(Ⅰ)解:由题
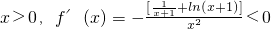
,…(2分)
故f(x)在区间(0,+∞)上是减函数;…(3分)
(Ⅱ)解:当x>0时,
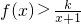
恒成立,即
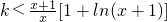
在(0,+∞)上恒成立,
取
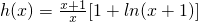
,则
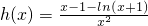
,…(5分)
再取g(x)=x-1-ln(x+1),则
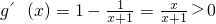
,
故g(x)在(0,+∞)上单调递增,
而g(1)=-ln2<0,g(2)=1-ln3<0,g(3)=2-2ln2>0,…(7分)
故g(x)=0在(0,+∞)上存在唯一实数根a∈(2,3),a-1-ln(a+1)=0,
故x∈(0,a)时,g(x)<0;x∈(a,+∞)时,g(x)>0,
故
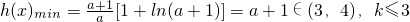
,故k
max=3…(8分)
(Ⅲ)证明:由(Ⅱ)知:
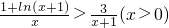
,∴
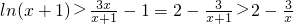
令
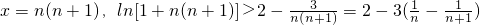
,…(10分)
又ln[(1+1•2)•(1+2•3)•(1+3•4)•…•(1+n(n+1))]=ln(1+1×2)+ln(1+2×3)+…+ln(1+n×(n+1))
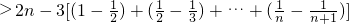
=
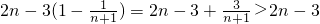
即:(1+1•2)•(1+2•3)•(1+3•4)•…•[1+n(n+1)]>e
2n-3…(14分)
分析:(Ⅰ)求导函数,确定导数的符号,即可得到结论;
(Ⅱ)当x>0时,
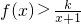
恒成立,即
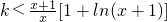
在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;
(Ⅲ)由(Ⅱ)知:
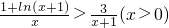
,从而令
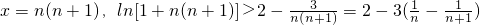
,即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查不等式的证明,属于中档题.

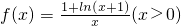 .
.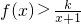 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;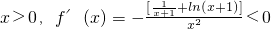 ,…(2分)
,…(2分)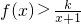 恒成立,即
恒成立,即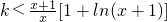 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,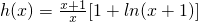 ,则
,则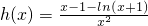 ,…(5分)
,…(5分)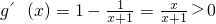 ,
,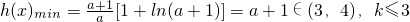 ,故kmax=3…(8分)
,故kmax=3…(8分)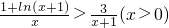 ,∴
,∴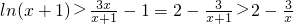
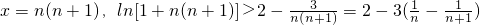 ,…(10分)
,…(10分)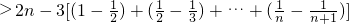 =
=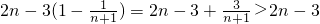
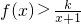 恒成立,即
恒成立,即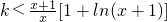 在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;
在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;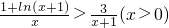 ,从而令
,从而令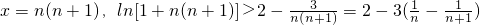 ,即可证得结论.
,即可证得结论.

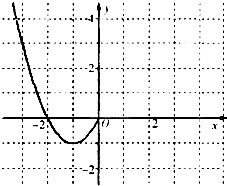 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.