
(1)求点P的轨迹曲线C的方程;
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;
(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且![]() =-3,求a的值.
=-3,求a的值.
(文)设函数f(x)=![]() x3+2ax2-3a2x+
x3+2ax2-3a2x+![]() a(0<a<1).
a(0<a<1).
(1)求函数f(x)的单调区间;
(2)若当x∈[a,2]时,恒有f(x)≤0,试确定实数a的取值范围.
答案:
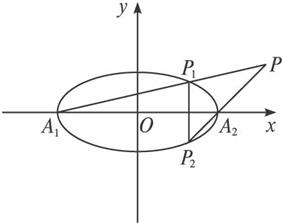
解:(1)设P1(m,n)(mn≠0),则P2(m,-n),直线A1P1:y=![]() (x+a);①直线A2P2:y=
(x+a);①直线A2P2:y=![]() (x-a);②
(x-a);②
设P点坐标为(x,y),由①②,得m=![]() ,
,
∵点P1(m,n)在椭圆![]() +y2=1上,∴有m2+a2n2=a2,即(
+y2=1上,∴有m2+a2n2=a2,即(![]() )2+a2(
)2+a2(![]() )2=a2,整理,得
)2=a2,整理,得![]() -y2=1(y≠0),∴直线A1P1与直线A2P2交点P的轨迹方程是双曲线
-y2=1(y≠0),∴直线A1P1与直线A2P2交点P的轨迹方程是双曲线![]() -y2=1(y≠0).
-y2=1(y≠0).
(2)由C与l相交于两个不同的点,知方程组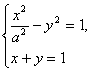 有两个不同的实数解.消去y并整理,得(1-a2)x2+2a2x-2a2=0.又∵a>0且a≠1,∴4a4+8a2(1-a2)>0.∴0<a2<2且a2≠1.
有两个不同的实数解.消去y并整理,得(1-a2)x2+2a2x-2a2=0.又∵a>0且a≠1,∴4a4+8a2(1-a2)>0.∴0<a2<2且a2≠1.
双曲线的离心率e=![]() .
.
∴![]() 或e>
或e>![]() ,即e∈(
,即e∈(![]() )∪(
)∪(![]() ,+∞).
,+∞).
(3)设A(x1,y1)、B(x2,y2),则-3=![]() =x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1
=x1x2+y1y2=x1x2+(1-x1)(1-x2)=2x1x2-(x1+x2)+1
=![]() +1,即
+1,即![]() =-4,由a>0,得a=
=-4,由a>0,得a=![]() .
.
(文)解:(1)∵f(x)=-![]() x3+2ax2-3a2x+
x3+2ax2-3a2x+![]() a(0<a<1),
a(0<a<1),
∴f′(x)=-x2+4ax-3a2=-(x-a)(x-3a).
∵0<a<1,∴f′(x)>0![]() a<x<3a,f′(x)<0
a<x<3a,f′(x)<0![]() x<a或x>3a.
x<a或x>3a.
∴函数f(x)的递增区间为[a,3a];递减区间为(-∞,a],[3a,+∞).
(2)∵x∈[a,2],①当2≤3a,即![]() ≤a<1时,f(x)在区间[a,2]内是增函数.
≤a<1时,f(x)在区间[a,2]内是增函数.
∴f(x)max=f(2)=![]() a-6a2.又当x∈[a,2]时,恒有f(x)≤0,
a-6a2.又当x∈[a,2]时,恒有f(x)≤0,
∴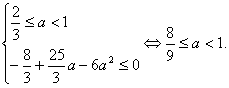
②当2>3a即0<a<![]() 时,则f(x)在[a,3a]上单调递增;在[3a,2]上单调递减.
时,则f(x)在[a,3a]上单调递增;在[3a,2]上单调递减.
∴f(x)max=f(3a)=![]() a.又当x∈[a,2]时,恒有f(x)≤0,∴
a.又当x∈[a,2]时,恒有f(x)≤0,∴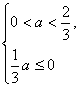 (无解).
(无解).
综上所述,a的取值范围是![]() ≤a<1.
≤a<1.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
| x2 |
| 4 |
| 2 |
| OA |
| OB |
| OM |
| 1 |
| 2 |
| OP1 |
| OP2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求点P的轨迹曲线C的方程;
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;
(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且![]() =-3,求a的值.
=-3,求a的值.
(文)(本小题满分12分)设函数f(x)=![]() x3+2ax2-3a2x+
x3+2ax2-3a2x+![]() a(0<a<1).
a(0<a<1).
(1)求函数f(x)的单调区间;
(2)若当x∈[a,2]时,恒有f(x)≤0,试确定实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| 4 |
| 2 |
| OA |
| OB |
| OM |
| 1 |
| 2 |
| OP1 |
| OP2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)判断函数f(x)在区间(0,+∞)上的单调性,证明你的结论;
(2)若当x>0时,f(x)>![]() 恒成立,求正整数k的最大值.(参考数据:ln2≈0.7,ln3≈1.1)
恒成立,求正整数k的最大值.(参考数据:ln2≈0.7,ln3≈1.1)
(文) P1是椭圆![]() +y2=1(a>0且a≠1)上不与顶点重合的任一点,P1P2是垂直于x轴的弦,A1(-a,0),A2(a,0)是椭圆的两个端点,直线A1P1与直线A2P2交点为P.
+y2=1(a>0且a≠1)上不与顶点重合的任一点,P1P2是垂直于x轴的弦,A1(-a,0),A2(a,0)是椭圆的两个端点,直线A1P1与直线A2P2交点为P.
(1)求P点的轨迹曲线C的方程;
(2)设曲线C与直线l:x+y=1相交于两个不同的点A、B,求曲线C的离心率e的取值范围;
(3)设曲线C与直线l:x+y=1相交于两个不同的点A、B,O为坐标原点,且![]() =-3,求a的值.
=-3,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com