
分析 结合充要条件的定义,逐一分析给定的条件p与条件q的关系,可得结论.
解答 解:(1)p:$\frac{1}{x}<$1?x<0,或x>1,q:x>1,故p是q的必要不充分条件;
(2)b=0时函数y=ax2+c是偶函数,函数y=ax2+bx+c是偶函数时,b=0,则p是q的充要条件;
(3)k>0时,函数y=$\frac{k}{x}$在(-∞,0)上和(0,+∞)上是减函数,
函数y=$\frac{k}{x}$在(-∞,0)上和(0,+∞)上是减函数时,k>0,则p是q的充要条件;
(4)平行四边形的对角线相等时,这个平行四边形是矩形.
平行四边形是矩时,对角线相等,则p是q的充要条件;
点评 本题考查的知识点是充要条件的定义,熟练掌握并正确理解充要条件的定义是解答的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
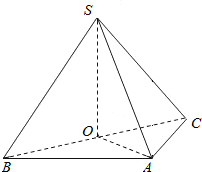 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{3}$,+∞) | B. | (0,$\frac{9}{16}$] | C. | (0.+∞) | D. | ($\frac{9}{16}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x${\;}^{\frac{4}{3}}$ | B. | x2 | C. | x3 | D. | x4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com