
如图,从边长为 的正方形铁皮的四个角各截去一个边长为
的正方形铁皮的四个角各截去一个边长为 的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度
的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度 与底面正方形的边长的比不超过常数
与底面正方形的边长的比不超过常数 ,问:
,问: 取何值时,长方体的容积V有最大值?
取何值时,长方体的容积V有最大值?

略
【解析】此题是一道应用题,主要还是考查导数的定义及利用导数来求区间函数的最值,利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力,解题的关键是求导要精确.
求体积最大值的问题,由题意解出v的表达式,对函数v进行求导,解出极值点,然后根据极值点来确定函数v的单调区间,
因极值点是关于a,t的表达式,此时就需要讨论函数v的单调性,分别代入求出最大值,从而求解.
解:长方体的体积V(x)=4x(x-a)2,(o<x<a),…………………………2分
由 ≤ t 得 0<x≤
≤ t 得 0<x≤ <
a …………………4分
<
a …………………4分
而V′=12(x- )(x-a) ∴V在(0,
)(x-a) ∴V在(0, )增,在(
)增,在( , a)递减……………6分
, a)递减……………6分


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源:2013-2014学年江西赣州市六校高三第一学期期末联考文科数学试卷(解析版) 题型:选择题
如图放置的边长为1的正方形 沿
沿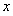 轴正方向滚动.设顶点
轴正方向滚动.设顶点 的轨迹方程是
的轨迹方程是 ,设
,设 在其两个相邻零点间的图象与
在其两个相邻零点间的图象与 轴所围区域为S,则直线
轴所围区域为S,则直线 从
从 所匀速移动扫过区域S的面积D与
所匀速移动扫过区域S的面积D与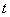 的函数图象大致为( ).
的函数图象大致为( ).





A. B. C. D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com