
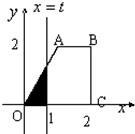
 如图在直角梯形OABC中AB∥OC,AB=1,OC=BC=2,直线l:x=t,t∈[0,2]截得此梯形所得位于l左方的图形面积为S,那么函数S=f(t)的图象大致可为下列图中的( )
如图在直角梯形OABC中AB∥OC,AB=1,OC=BC=2,直线l:x=t,t∈[0,2]截得此梯形所得位于l左方的图形面积为S,那么函数S=f(t)的图象大致可为下列图中的( )科目:高中数学 来源: 题型:
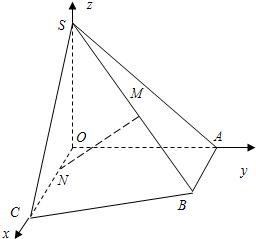 如图所示在直角梯形OABC中,∠COA=∠OAB=
如图所示在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在直角梯形OABC中,∠COA=∠OAB=
如图所示,在直角梯形OABC中,∠COA=∠OAB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省南京十三中高考数学模拟试卷(解析版) 题型:解答题
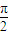 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,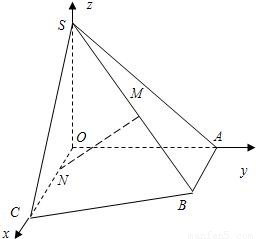
查看答案和解析>>
科目:高中数学 来源:2008年江苏省苏州五中高三调研数学试卷(解析版) 题型:解答题
 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,
查看答案和解析>>
科目:高中数学 来源:2011年高考数学附加题部分专项训练1(理科)(解析版) 题型:解答题
 ,OA=OS=AB=1,OC=4,
,OA=OS=AB=1,OC=4,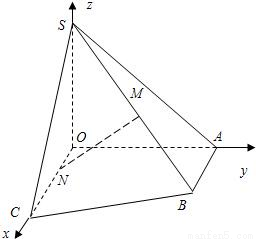
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com