
 ,目标函数
,目标函数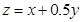 ,再作出不等式组表示的可行域,找出最优解,求出z的最大值.
,再作出不等式组表示的可行域,找出最优解,求出z的最大值. ,目标函数
,目标函数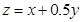 ,上述不等式组表示的平面区域如图所示,
,上述不等式组表示的平面区域如图所示,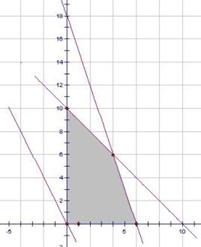
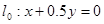 ,并作平行于直线
,并作平行于直线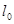 的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线
的一组直线,与可行域相交,其中有一条直线经过可行域上的点M,且与直线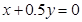 的距离最大,其中M点是直线
的距离最大,其中M点是直线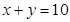 和直线
和直线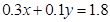 的交点,解方程组
的交点,解方程组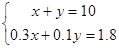 得
得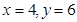 ,此时
,此时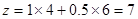 (万元),
(万元),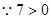 ,当
,当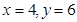 时,
时,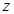 最得最大值.
最得最大值.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:不详 题型:单选题
| | A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com