
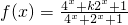
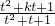 (t>0),
(t>0), )恒成立,
)恒成立, ≥2,∴-(t+
≥2,∴-(t+ )≤-2,
)≤-2, ,即t=1时,-(t+
,即t=1时,-(t+ )有最大值为-2,
)有最大值为-2,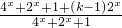 =1+
=1+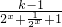 ,
,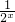 +1≥3,则y=1+
+1≥3,则y=1+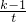 (t≥3),
(t≥3), ],无最小值,舍去;
],无最小值,舍去; ,1),
,1), =-3得k=-11;
=-3得k=-11;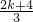 且1<f(x3)≤
且1<f(x3)≤ ,故
,故 ≤2,∴1<k≤4;
≤2,∴1<k≤4;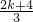 ≤f(x1)+f(x2)<2,且
≤f(x1)+f(x2)<2,且 ≤f(x3)<1,故
≤f(x3)<1,故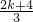 ≥1,∴-
≥1,∴- ≤k<1;
≤k<1; ≤k≤4.
≤k≤4.

科目:高中数学 来源:2013-2014学年江西师大附中高三年级上学期期中考试理科数学试卷(解析版) 题型:解答题
已知函数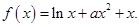
(1)若 在
在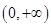 是增函数,求
是增函数,求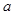 的取值范围;
的取值范围;
(2)已知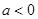 ,对于函数
,对于函数 图象上任意不同两点
图象上任意不同两点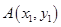 ,
,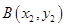 ,其中
,其中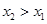 ,直线
,直线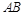 的斜率为
的斜率为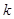 ,记
,记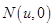 ,若
,若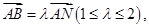 求证:
求证: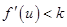 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省宿迁市沭阳县华冲中学高三(上)9月调研数学试卷(文科)(解析版) 题型:解答题
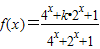
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省连云港市新海高级中学高三(下)3月调研数学试卷(解析版) 题型:解答题
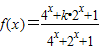
查看答案和解析>>
科目:高中数学 来源:江苏期末题 题型:解答题
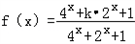
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com