
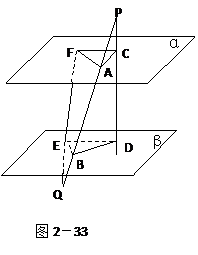
 如图2-33:线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,
如图2-33:线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,![]() ACF的面积为72,求
ACF的面积为72,求![]() BDE的面积。
BDE的面积。
求![]() BDE的面积,看起来似乎与本节内容无关,事实上,已知
BDE的面积,看起来似乎与本节内容无关,事实上,已知![]() ACF的面积,若
ACF的面积,若![]() BDE与
BDE与![]() ACF的对应边有联系的话,可以利用
ACF的对应边有联系的话,可以利用![]() ACF的面积求出
ACF的面积求出![]() BDE的面积。
BDE的面积。
(提示:①![]() ABC的两条邻边分别长为a、b,夹角为θ,则
ABC的两条邻边分别长为a、b,夹角为θ,则![]() ABC的面积S=
ABC的面积S=![]() absinθ,②sinα=sin(180°-α)
absinθ,②sinα=sin(180°-α)
∵平面QAF∩α=AF,平面QAF∩β=BE,又∵α∥β,∴AF∥BE
同理可证:AC//BD,∴∠FAC与∠EBD相等或互补,即sin∠FAC= sin∠EBD.
由 AF∥BE,得![]() ,∴BE=
,∴BE=![]() AF
AF
由BD//AC,得:![]() ,∴BD=
,∴BD=![]() AC
AC
又∵![]() ACF的面积为72,即
ACF的面积为72,即![]() AF·AC·sin∠FAC=72,
AF·AC·sin∠FAC=72,
∴![]() =
=![]() BE·BD·sin∠EBD
BE·BD·sin∠EBD
=![]() ·
·![]() AF·
AF·![]() AC·sin∠FAC
AC·sin∠FAC
=![]() ·
·![]() AF·AC·sin∠FAC=
AF·AC·sin∠FAC=![]() ×72=84
×72=84
∴![]() BDE的面积为84平方单位。
BDE的面积为84平方单位。


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
 (2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
(2012•湖南)函数f(x)=sin (ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,P为图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.| π |
| 6 |
3
| ||
| 2 |
 |
| ABC |
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
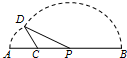 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )查看答案和解析>>
科目:高中数学 来源: 题型:
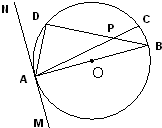 (几何证明选讲)如图,半径是3
(几何证明选讲)如图,半径是3| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com