
在今年伦敦奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是 .
.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率.
(Ⅲ)设随机变量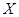 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求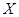 的分布列及期望
的分布列及期望
(Ⅰ)来自美国的2人,来自英国的4人.(Ⅱ)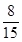 (Ⅲ)期望:
(Ⅲ)期望: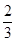 ,分布列见解析
,分布列见解析
【解析】(I) 按照对立事件来求.设至少一名美国志愿者被分到跳水岗位为事件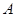 ,则
,则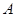 的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人
的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人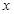 个,则
个,则 得到关于x的方程,求出x的值.
得到关于x的方程,求出x的值.
可得美国、英国的人数.
(II)篮球岗位恰好美国人、英国人各有一人,因为美国为2人,英国的4人,则 .
.
(III) 设随机变量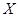 为在体操岗位服务的美国志愿者的个数,
为在体操岗位服务的美国志愿者的个数, 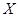 的所有可能值为0,1,2,
的所有可能值为0,1,2,
然后分别求出X对应值的概率,列出分布列,求出数学期望即可.
解:(Ⅰ)记至少一名美国志愿者被分到跳水岗位为事件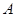 ,则
,则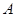 的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人
的对立事件为“没有美国志愿者被分到跳水岗位”,设有美国人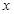 个,
个,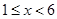 ,那么
,那么 ,解得
,解得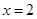 ,即来自美国的2人,来自英国的4人. (4分)
,即来自美国的2人,来自英国的4人. (4分)
(Ⅱ)记篮球岗位恰好美国人、英国人各有一人为事件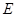 ,那么
,那么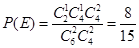 ,
,
所以篮球岗位恰好美国人、英国人各一人的概率是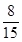 .
(8分)
.
(8分)
(3)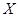 的所有可能值为0,1,2,
的所有可能值为0,1,2,
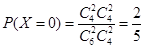 ,
,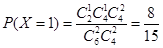 ,
,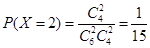 ,故有分布列:
,故有分布列:
 ……………(10分)
……………(10分)
从而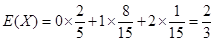 (人).
(12分)
(人).
(12分)


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com