练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若方程2（k2-2）x2+k2y2+k2-k-6=0表示椭圆，则k的取值范围是（　　）
    分析：利用椭圆的标准方程即可得出．
    解答：解：方程2（k2-2）x2+k2y2+k2-k-6=0化为
    x2
    6+k-k2
    2(k2-2)
    +
    y2
    6+k-k2
    k2
    =1．
    ∵方程2（k2-2）x2+k2y2+k2-k-6=0表示椭圆，
    ∴
    6+k-k2
    2(k2-2)
    ＞0
    6+k-k2
    2(k2-2)
    ≠
    6+k-k2
    k2
    6+k-k2
    k2
    ＞0
    ，解得-2＜k＜-
    		2
    ，且
    		2
    ＜k＜3    ，且k≠2．
    故选D．
    点评：熟练掌握椭圆的标准方程是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省临清三中2011-2012学年高二12月月考数学试题 题型：044

    已知抛物线y2＝4x和点，过点P的直线l与抛物线交与A，B两点，设点P刚好为弦AB的中点．

    (1)求直线l的方程

    (2)若过线段AB上任一P1(不含端点A，B)作倾斜角为π－arctan2的直线l交抛物线于A1，B1，类比圆中的相交弦定理，给出你的猜想，若成立，给出证明；若不成立，请说明理由．

    (3)过P作斜率分别为k1，k2(k1≠k2)的直线l1，l2，l1交抛物线于A1，B1，l2交抛物线于A2，B2，是否存在k1，k2(k1≠k2)使得(2)中的猜想成立，若存在，给出k1，k2满足的条件．若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省高三第三次（3月）周测理科数学试卷（解析版） 题型：选择题

    下列命题中正确的有

    ①设有一个回归方程=2—3x，变量x增加一个单位时，y平均增加3个单位；

    ②命题P：“”的否定P：“”；

    ③设随机变量X服从正态分布N(0，1)，若P(X>1)=p，则P(-1<X<0)=-p；

    ④在一个2×2列联表中，由计算得k2=6．679，则有99％的把握确认这两个变量间有关系．

    A．1个             B．2个              C．3个              D．4个

    本题可以参考独立性检验临界值表

    P(K2≥k)

    0.5

    0.40

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    0.455

    0.708

    1.323

    2.072

    2.706

    3.841

    5.024

    6.535

    7.879

    10.828

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设椭圆C:=1(a＞b＞0)过点(1,),F1、F2分别为椭圆C的左、右两个焦点,且离心率e=.

    (1)求椭圆C的方程;

    (2)已知A为椭圆C的左顶点,直线l过右焦点F2与椭圆C交于M、N两点.若AM,AN的斜率k1,k2满足k1+k2=,求直线l的方程;

    (3)已知P是椭圆C上位于第一象限内的点,△PF1F2的重心为G,内心为I,求证:GI∥F1F2.

    查看答案和解析>>

    科目：高中数学 来源：2006-2007学年江苏省苏州市五县地区高二（上）期末数学试卷（解析版） 题型：选择题

    若方程2（k2-2）x2+k2y2+k2-k-6=0表示椭圆，则k的取值范围是（ ）
    A．
    B．
    C．（-2，3 ）
    D．

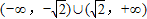
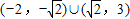
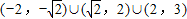
    查看答案和解析>>

    同步练习册答案