
已知圆 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足 (
( 为参数).
为参数).
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)若 求直线
求直线 的方程;
的方程;
(3)求实数 的取值范围.
的取值范围.
(1) 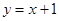 或
或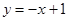 (2)
(2)  (3)
(3) 
【解析】本试题主要是考查了直线与圆位置关系的运用。以及直线方程的求解和参数的求值问题。
(1)因为当直线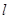 的斜率不存在时,
的斜率不存在时,
 ,不满足,故可设所求直线
,不满足,故可设所求直线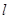 的方程为
的方程为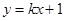 与圆的方程联立,结合韦达定理得到结论。
与圆的方程联立,结合韦达定理得到结论。
(2)设直线方程与圆联立,然后结合向量的关系式得到坐标关系,并结合韦达定理得到参数k的值,进而得到直线的方程。
(3)可设所求直线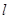 的方程为
的方程为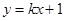 ,
,
代入圆的方程,整理得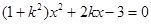 ,(*)
,(*)
设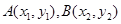 ,则
,则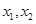 为方程(*)的两根,
为方程(*)的两根,
由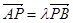 可得
可得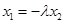
则有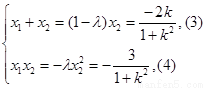 ,
,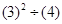 得
得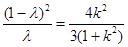 , ----(12分)
, ----(12分)
而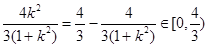 ,由
,由 可解得
可解得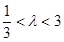
所以实数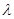 的取值范围为可得。
的取值范围为可得。
解:(I)当直线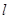 的斜率不存在时,
的斜率不存在时,
 ,不满足,故可设所求直线
,不满足,故可设所求直线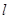 的方程为
的方程为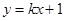 , ------------(1分)
, ------------(1分)
代入圆的方程,整理得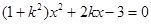 , --------------(2分)
, --------------(2分)
利用弦长公式可求得直线方程为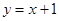 或
或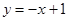 .--------------(4分)
.--------------(4分)
(II)当直线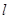 的斜率不存在时,
的斜率不存在时,
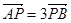 或
或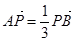 ,不满足,故可设所求直线
,不满足,故可设所求直线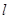 的方程为
的方程为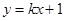 , ---------------(5分)
, ---------------(5分)
代入圆的方程,整理得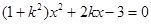 ,
,
设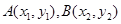 ,则
,则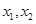 为方程(*)的两根,
为方程(*)的两根,
由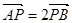 可得
可得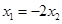 ---------(6分)
---------(6分)
则有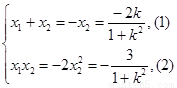 ,
,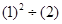 得
得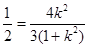 ,解得
,解得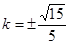 ---(8分)
---(8分)
所以直线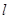 的方程为
的方程为 -------------(9分)
-------------(9分)
(III)当直线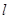 的斜率不存在时,
的斜率不存在时,
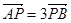 或
或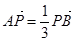 ,
,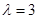 或
或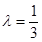 ,---------(10分)
,---------(10分)
当直线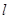 的斜率存在时可设所求直线
的斜率存在时可设所求直线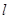 的方程为
的方程为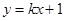 ,
,
代入圆的方程,整理得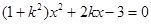 ,(*)
,(*)
设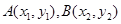 ,则
,则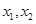 为方程(*)的两根,
为方程(*)的两根,
由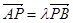 可得
可得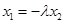
则有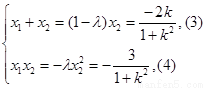 ,
,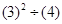 得
得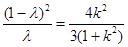 , -----(12分)
, -----(12分)
而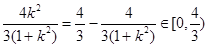 ,由
,由 可解得
可解得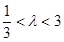
所以实数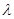 的取值范围为
的取值范围为 -----------(14分)
-----------(14分)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届吉林省白山市高一下学期期末考试文科数学卷(解析版) 题型:解答题
已知圆 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足 (
( 为参数).
为参数).
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)若 求直线
求直线 的方程;
的方程;
(3)求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com