
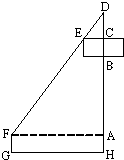
 如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)
如图,在某建筑工地上有一个吊臂长DF=24m的吊车,吊车底座FG高1.m.现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上.(注:当物件与吊臂接触后,钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触,且与工件的中心在一条垂直线上.)| 3 |
| π |
| 2 |
| π |
| 2 |
| 3 |
| cos2θ |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| 3 |
| cos2θ |
| 24cos3θ-3 |
| cos2θ |
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
| 3 |
| cos2θ |
| 24cos3θ-3 |
| cos2θ |
| π |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
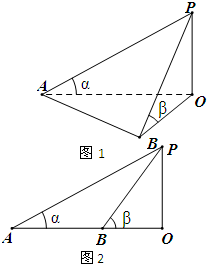 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.| 4 | d |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 2 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.
如图1,某学校田径场上有一旗杆OP,为了测量它的高度,在地面上选一基线AB,设其长度为d,在A点处测得P点的仰角为α,在B点处测得P点的仰角为β.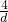 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省常德市芷兰实验学校高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 ,旗杆的实际高度为25,试问d为何值时,β-α最大?
,旗杆的实际高度为25,试问d为何值时,β-α最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com