
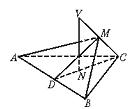
如图,已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上.AB=a,VC与AB之间的距离为h,点M∈VC.
(Ⅰ)证明∠MDC是二面角M—AB—C的平面角;
(Ⅱ)当∠MDC=∠CVN时,证明VC⊥平面AMB;
(Ⅲ)若∠MDC=∠CVN=θ(0<θ<![]() =,求四面体MABC的体积.
=,求四面体MABC的体积.
科目:高中数学 来源: 题型:
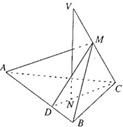 19、如图已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上.AB=a,VC与AB之间的距离为h,点M∈VC.
19、如图已知VC是△ABC所在平面的一条斜线,点N是V在平面ABC上的射影,且在△ABC的高CD上.AB=a,VC与AB之间的距离为h,点M∈VC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
如图,已知AB是⊙O的直径,点C是⊙O上的动点(异于A、B),过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
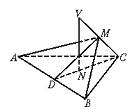
(Ⅰ)证明∠MDC是二面角M—AB—C的平面角;
(Ⅱ)当∠MDC=∠CVN时,证明VC⊥平面AMB;
(Ⅲ)若∠MDC=∠CVN=θ(0<θ<![]() =,求四面体MABC的体积.
=,求四面体MABC的体积.
查看答案和解析>>
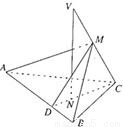
科目:高中数学 来源:2001年北京市高考数学试卷(理)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com