
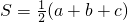 r.若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体类似的结论为________.
r.若四面体四个面的面积分别为S1,S2,S3,S4,内切球的半径为R,则此四面体类似的结论为________. (S1+S2+S3+S4)R
(S1+S2+S3+S4)R (S1+S2+S3+S4)R.接下来可以用体积分割的方法,类似地证明推广到空间的结论也是正确的.
(S1+S2+S3+S4)R.接下来可以用体积分割的方法,类似地证明推广到空间的结论也是正确的.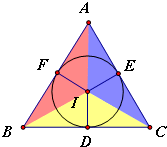 设△ABC的内切圆圆心为I,圆I与BC、CA、AB分别相切于点D、E、F,
设△ABC的内切圆圆心为I,圆I与BC、CA、AB分别相切于点D、E、F, BC•ID=
BC•ID= ar,
ar, AC•IE=
AC•IE= br,S△IAB=
br,S△IAB= AB•IF=
AB•IF= cr,
cr, ar+
ar+ br+
br+ cr=
cr=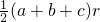
 (S1+S2+S3+S4)R.
(S1+S2+S3+S4)R. S△BCD•OE=
S△BCD•OE= S1R,
S1R, S△ACD•OF=
S△ACD•OF= S2R,三棱锥O-ABD的体积为V3=
S2R,三棱锥O-ABD的体积为V3= S△ABD•OG=
S△ABD•OG= S3R,
S3R, S△ABC•OH=
S△ABC•OH= S4R
S4R S1R+
S1R+ S2R+
S2R+ S3R+
S3R+ S4R=
S4R= (S1+S2+S3+S4)R.
(S1+S2+S3+S4)R. (S1+S2+S3+S4)R
(S1+S2+S3+S4)R

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市梁山一中高二(下)3月月考数学试卷(理科)(解析版) 题型:选择题
 >
>
 <
<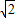
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com