
 ,acosA=bcosB.
,acosA=bcosB.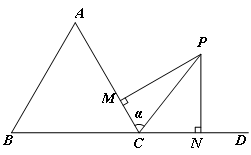
 ,(2)2
,(2)2 .
. .又因为C=
.又因为C= ,得A+B=
,得A+B= ,与A+B=
,与A+B= 矛盾,所以A=B,因此A=
矛盾,所以A=B,因此A= .(2)求PM+PN的最大值,需先将PM+PN表示为α的函数解析式. 在Rt△PMC中,PM=PC·sin∠PCM=2sinα;在Rt△PNC中,PN=PC·sin∠PCN= PC·sin(π-∠PCB) =2sin[π-(α+
.(2)求PM+PN的最大值,需先将PM+PN表示为α的函数解析式. 在Rt△PMC中,PM=PC·sin∠PCM=2sinα;在Rt△PNC中,PN=PC·sin∠PCN= PC·sin(π-∠PCB) =2sin[π-(α+ )]=2sin (α+
)]=2sin (α+ ),α∈(0,
),α∈(0, ),所以,PM+PN=2sinα+2sin (α+
),所以,PM+PN=2sinα+2sin (α+ )=3sinα+
)=3sinα+ cosα=2
cosα=2 sin(α+
sin(α+ ).因为α∈(0,
).因为α∈(0, ),所以α+
),所以α+ ∈(
∈( ,
, ),从而有sin(α+
),从而有sin(α+ )∈(
)∈( ,1],即2
,1],即2 sin(α+
sin(α+ )∈(
)∈( ,2
,2 ].于是,当α+
].于是,当α+ =
= ,即α=
,即α= 时,PM+PN取得最大值2
时,PM+PN取得最大值2 .
. . 3分
. 3分  ,得A+B=
,得A+B= ,与A+B=
,与A+B= 矛盾,
矛盾, . 6分
. 6分 )]=2sin (α+
)]=2sin (α+ ),α∈(0,
),α∈(0, ). 8分
). 8分 )=3sinα+
)=3sinα+ cosα=2
cosα=2 sin(α+
sin(α+ ). 12分
). 12分 ),所以α+
),所以α+ ∈(
∈( ,
, ),从而有sin(α+
),从而有sin(α+ )∈(
)∈( ,1],
,1], sin(α+
sin(α+ )∈(
)∈( ,2
,2 ].
]. =
= ,即α=
,即α= 时,PM+PN取得最大值2
时,PM+PN取得最大值2 . 16分
. 16分

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源:不详 题型:解答题
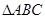 中,
中,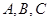 的对边分别为
的对边分别为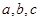 且
且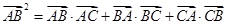 .
.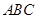 的形状,并求
的形状,并求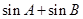 的取值范围;
的取值范围;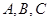 的顶点
的顶点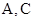 分别在
分别在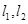 上运动,
上运动,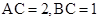 ,若直线
,若直线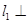 直线
直线 ,且相交于点
,且相交于点 ,求
,求 间距离的取值范围.
间距离的取值范围.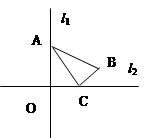
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com