
 本题满分13分
本题满分13分 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(I)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.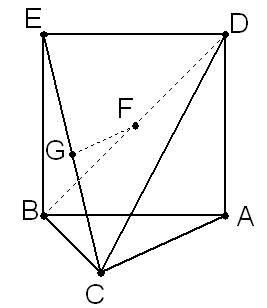
解:(I)证法一:取BE的中点H,连结HF、GH,(如图1) 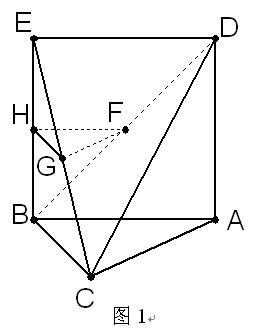
∵G、F分别是EC和BD的中点
∴HG//BC,HF//DE,……………… 2分
又∵ADEB为正方形 ∴DE//AB,从而HF//AB
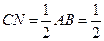 , ………………11分
, ………………11分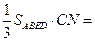
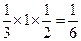 ………………13分
………………13分
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (本题满分13分) 如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),
(本题满分13分) 如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进.现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个1、两个2、两个3一共六个数字.质点P从A点出发,规则如下:当正方体上底面出现的数字是1,质点P前进一步(如由A到B);当正方体上底面出现的数字是2,质点P前进两步(如由A到C),
当正方体上底面出现的数字是3,质点P前进三步(如由A到![]() ).
).
在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(Ⅰ)求点P恰好返回到A点的概率;
(Ⅱ)在点P转一圈恰能返回到A点的所有结果中,
用随机变量![]() 表示点P恰能返回到A点的投掷次数,求
表示点P恰能返回到A点的投掷次数,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期第二次月考理科数学试卷(解析版) 题型:解答题
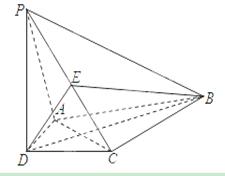
(本题满分13分)如图所示,在四棱锥 中,
中, 平面
平面 ,
,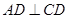 ,
,
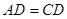 ,
,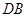 平分
平分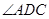 ,
,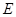 为
为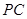 的中点.
的中点.
求证:(1)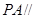 平面
平面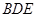 ;
;
(2)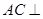 平面
平面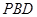 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省高三上学期第三次月考理科数学卷 题型:解答题
(本题满分13分)
如图,在六面体 中,平面
中,平面 ∥平面
∥平面 ,
,
⊥平面 ,
, ,
, ,
,
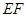 ∥
∥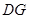 .且
.且 ,
, .
.
(1)求证:  ∥平面
∥平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3) 求五面体 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市东城区高三年级十校联考文科数学 题型:解答题
 本题满分13分
本题满分13分 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(I)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com