Question

下表给出一个“等差数阵”．

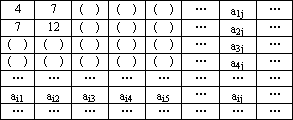
其中每行、每列都是等差数列，a_ij表示位于第i行第j列的数．

(1)写出a₄₅的值．

(2)写出a_ij的计算公式．

(3)证明正整数N在该等差数阵中的充要条件是2N＋1可以写成两个不是1的正整数之积．

Answer 1

答案：
解析：

解：(1)a41＝a11＋(4－1)×3＝13 　　a42＝a12＋(4－1)×5＝22 　　a45＝a41＋(5－1)×9＝49 　　(2)ai1＝a11＋(i－1)×3＝3i＋1 　　ai2＝a12＋(i－1)×5＝5i＋2 　　aij＝ai1＋(j－1)×(2i＋1)＝i＋j＋2ij 　　(3)若N是该数阵中的数，则可令N＝aij 　　故N＝i＋j＋2ij(i，j∈N*) 　　∴2N＋1＝2i＋2j＋4ij＋1＝(2i＋1)(2j＋1) 　　∴2N＋1能写成两个不是1的正整数之积． 　　若2N＋1＝p·q，N、p、q都是正整数， 　　且p、q不为1． 　　∵2N＋1是奇数，∴p、q都是奇数． 　　不妨设p＝2i＋1，q＝2j＋1，i，j∈N* 　　∴2N＋1＝(2i＋1)(2j＋1) 　　N＝i＋j＋2ij＝aij 　　∴N是该数阵中第i行第j列的数．