
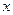
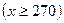 元,月收益为
元,月收益为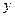 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。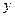 与
与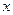 的函数关系式;
的函数关系式;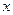 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少? 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:不详 题型:解答题
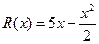 (万元)
(万元)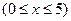 ,其中
,其中
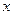 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
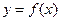 的定义域为
的定义域为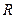 ,当
,当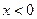 时,
时,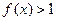 ,且对任意的实数
,且对任意的实数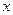 ,
,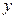
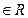 ,
,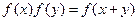 恒成立.若数列{
恒成立.若数列{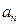 }满足
}满足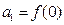 ,且
,且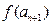 =
=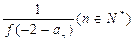 ,
,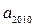 的值为
的值为 | A.4016 | B.4017 | C.4018 | D.4019 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
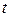 | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 | ||||||||||||
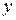 | 1.5 | 4.04 | 7.5 | 12 | 18.01
查看答案和解析>> 科目:高中数学 来源:不详 题型:单选题 .若设函数 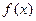 的定义域为D,若存在非零实数 的定义域为D,若存在非零实数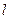 使得对于任意 使得对于任意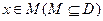 ,有 ,有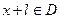 ,且 ,且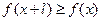 ,则称 ,则称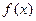 为M上的 为M上的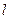 高调函数如果定义域为R的函数 高调函数如果定义域为R的函数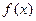 是奇函数,当 是奇函数,当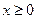 时, 时,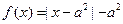 ,且 ,且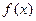 为R上的4高调函数,那么实数 为R上的4高调函数,那么实数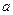 的取值范围是 ( ) 的取值范围是 ( )
查看答案和解析>> 科目:高中数学 来源:不详 题型:单选题 对于任意两个实数对(a,b),(c,d  ),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y) ),定义运算"⊙"为(a,b)⊙(c,d)=(a+c,bd),且(x,1)⊙(2,y) =(4,2),则(x,y)为. =(4,2),则(x,y)为.
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |