
【题目】已知圆C:(x﹣1)2+(y﹣1)2=1上存在4个点到直线x+y﹣m=0(m∈R)的距离等于1﹣ ![]() .
.
(1)求m的取值范围;
(2)判断圆C与圆D:x2+y2﹣2mx=0的位置关系.
【答案】
(1)解:圆的半径为r=1,
∵圆上存在4个点到直线x+y﹣m=0(m∈R)的距离等于1﹣ ![]() .
.
∴圆心(1,1)到直线的距离d< ![]() ,
,
即 ![]() <
< ![]() ,解得1<m<3
,解得1<m<3
(2)解:圆D的圆心为D(m,0),半径为|m|=m,
∴两圆的圆心距为 ![]() ,
,
∵1<m<3,
∴m﹣1< ![]() <m+1,
<m+1,
∴圆C与圆D相交
【解析】(1)由圆上存在4个点到直线x+y﹣m=0(m∈R)的距离等于![]() ,可得圆心到直线的距离d<
,可得圆心到直线的距离d<![]() ,再应用点到直线的距离公式即可;
,再应用点到直线的距离公式即可;
(2)应用圆心距与半径之间的关系判断圆与圆的位置关系即可;
【考点精析】解答此题的关键在于理解直线与圆的三种位置关系的相关知识,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


科目:高中数学 来源: 题型:
【题目】己知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名大学生尝试开家“网店”销售一种学习用品,经测算每售出1盒该产品可获利30元,未售出的商品每盒亏损10元.根据统计资料,得到该商品的月需求量的频率分布直方图如图所示,该同学为此购进180盒该产品,以x(单位:盒,100≤x≤200)表示一个月内的市场需求量,y(单位:元)表示一个月内经销该产品的利润.
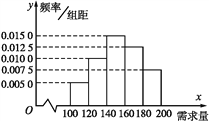
(1)根据直方图估计这个月内市场需求量x的平均数;
(2)将y表示为x的函数;
(3)根据直方图估计这个月利润不少于3 800元的概率(用频率近似概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“互联网+交通”模式的迅猛发展,“共享自行车”在很多城市相继出现.某运营公司为了了解某地区用户对其所提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:

用系统抽样法从40名用户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若用户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.试应用样本估计总体的思想,估计该地区满意度等级为“
级”.试应用样本估计总体的思想,估计该地区满意度等级为“![]() 级”的用户所占的百分比是多少?(精确到
级”的用户所占的百分比是多少?(精确到![]() )
)
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,BC边上的高所在的直线方程为x﹣2y+1=0,∠A的平分线所在直线的方程为y=0.
(1)求点A的坐标;
(2)若点B的坐标为(1,2),求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某创业投资公司拟开发某种新能源产品,估计能获得![]() 万元到
万元到![]() 万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金
万元的投资利益,现准备制定一个对科研课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过收益的
万元,同时奖金不超过收益的![]() .
.
(![]() )请分析函数
)请分析函数![]() 是否符合公司要求的奖励函数模型,并说明原因.
是否符合公司要求的奖励函数模型,并说明原因.
(![]() )若该公司采用函数模型
)若该公司采用函数模型![]() 作为奖励函数模型,试确定最小正整数
作为奖励函数模型,试确定最小正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据IEC(国际电工委员会)调查显示,小型风力发电项目投资较少,且开发前景广阔,但受风力自然资源影响,项目投资存在一定风险.根据测算,风能风区分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5~10 | 6.5~8.5 |
假设投资A项目的资金为x(x≥0)万元,投资B项目资金为y(y≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利30%的可能性为0.6,亏损20%的可能性为0.4;位于二类风区的B项目获利35%的可能性为0.6,亏损10%的可能性是0.1,不赔不赚的可能性是0.3.
(1)记投资A,B项目的利润分别为ξ和η,试写出随机变量ξ与η的分布列和期望Eξ,Eη;
(2)某公司计划用不超过100万元的资金投资于A,B项目,且公司要求对A项目的投资不得低于B项目,根据(1)的条件和市场调研,试估计一年后两个项目的平均利润之和z=Eξ+Eη的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com