
在直角坐标系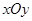 中,点
中,点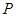 到两点
到两点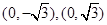 的距离之和等于4,设点
的距离之和等于4,设点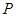 的轨迹为
的轨迹为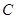 ,直线
,直线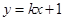 与
与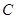 交于
交于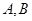 两点.
两点.
(1)写出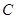 的方程;
的方程;
(2)若点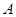 在第一象限,证明当
在第一象限,证明当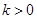 时,恒有
时,恒有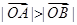 .
.
(1)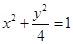 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)根据椭圆的定义,可判断点的轨迹为椭圆,再根据椭圆的基本量,容易写出椭圆的方程,求曲线的方程一般可设动点坐标为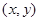 ,然后去探求动点坐标满足的方程,但如果根据特殊曲线的定义,先行判断出曲线的形状(如椭圆,圆,抛物线等),则可直接写出其方程;(2)一般地,涉及直线与二次曲线相交的问题,则可联立方程组,或解出交点坐标,或设而不求,利用一元二次方程根与系数的关系建立关系求出参数的值(取值范围),本题可设
,然后去探求动点坐标满足的方程,但如果根据特殊曲线的定义,先行判断出曲线的形状(如椭圆,圆,抛物线等),则可直接写出其方程;(2)一般地,涉及直线与二次曲线相交的问题,则可联立方程组,或解出交点坐标,或设而不求,利用一元二次方程根与系数的关系建立关系求出参数的值(取值范围),本题可设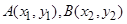 ,根据两点坐标满足的方程,去判断
,根据两点坐标满足的方程,去判断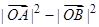 的符号.
的符号.
试题解析:(1)设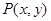 ,由椭圆定义可知,点
,由椭圆定义可知,点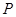 的轨迹
的轨迹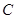 是以
是以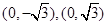 为焦点,长半轴为2的椭圆,它的短半轴
为焦点,长半轴为2的椭圆,它的短半轴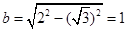 , 2分
, 2分
故曲线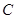 的方程为
的方程为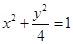 . 5分
. 5分
(2)证明:设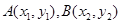 ,其坐标满足
,其坐标满足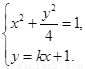 消去
消去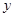 并整理,得
并整理,得
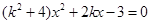 7分
7分
故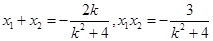 .
9分
.
9分
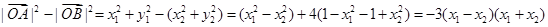
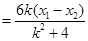 .
11分
.
11分
因为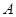 在第一象限,故
在第一象限,故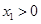 .
.
由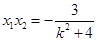 知
知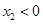 ,从而
,从而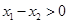 .
.
又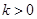 ,故
,故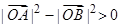 ,
,
即在题设条件下,恒有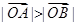 .
13分
.
13分
考点:椭圆的方程,直线与椭圆的位置关系.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源:2012-2013学年河北省高二第三次考试数学试卷(解析版) 题型:解答题
(本题满分12分)
在直角坐标系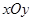 中,点
中,点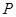 到两点
到两点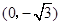 ,
,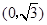 的距离之和等于
的距离之和等于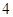 ,设点
,设点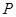 的轨迹为
的轨迹为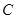 。
。
(1)求曲线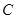 的方程;
的方程;
(2)过点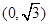 作两条互相垂直的直线
作两条互相垂直的直线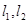 分别与曲线
分别与曲线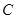 交于
交于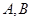 和
和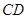 。
。
①以线段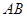 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的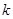 值,若不能说明理由;
值,若不能说明理由;
②求四边形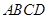 面积的取值范围。
面积的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第三次模拟考试文科数学试卷 题型:解答题
(本题满分14分)
在直角坐标系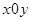 中,点
中,点 到两点
到两点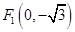 、
、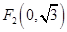 的距离之和等于4,设点
的距离之和等于4,设点 的轨迹为曲线
的轨迹为曲线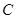 ,直线
,直线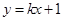 与曲线
与曲线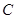 交于
交于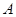 、
、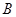 两点.
两点.
(1)求出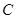 的方程;
的方程;
(2)若 =1,求
=1,求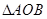 的面积;
的面积;
(3)若OA⊥OB,求实数 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三暑期教学质量检测文科数学 题型:解答题
(本题满分15分) 在直角坐标系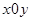 中,点
中,点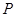 到两点
到两点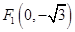 、
、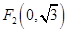 的距离之和等于4,设点
的距离之和等于4,设点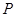 的轨迹为曲线
的轨迹为曲线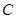 ,直线
,直线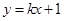 与曲线
与曲线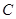 交于
交于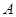 、
、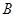 两点.
两点.
(1)求出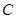 的方程;
的方程;
(2)若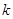 =1,求
=1,求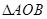 的面积
的面积
(3)若OA⊥OB,求实数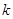 的值
的值
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试1-文科 题型:解答题
在直角坐标系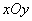 中,点
中,点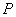 到两点
到两点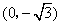 ,
,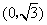 的距离之和等于
的距离之和等于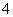 ,设点
,设点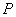 的轨迹为
的轨迹为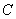 。
。
(1)求曲线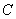 的方程;
的方程;
(2)过点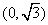 作两条互相垂直的直线
作两条互相垂直的直线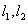 分别与曲线
分别与曲线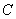 交于
交于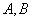 和
和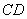 。
。
①以线段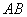 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的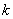 值,若不能说明理由;
值,若不能说明理由;
②求四边形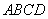 面积的取值范围。
面积的取值范围。
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三下学期数学单元测试1-理科 题型:解答题
在直角坐标系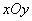 中,点
中,点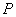 到两点
到两点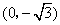 ,
,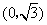 的距离之和等于
的距离之和等于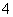 ,设点
,设点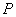 的轨迹为
的轨迹为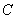 。
。
(1)求曲线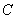 的方程;
的方程;
(2)过点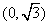 作两条互相垂直的直线
作两条互相垂直的直线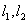 分别与曲线
分别与曲线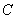 交于
交于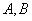 和
和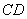 。
。
①以线段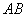 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的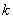 值,若不能说明理由;
值,若不能说明理由;
②求四边形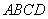 面积的取值范围。
面积的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com