

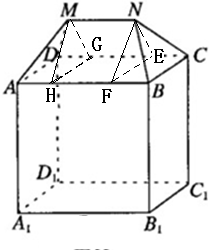
 EF=
EF=
 (AB-MN)=
(AB-MN)= (4-2)=1.
(4-2)=1.
 .
. =
=
 ,EF=2,∴∠ENF=90°
,EF=2,∴∠ENF=90° ×2×1×2=2,
×2×1×2=2, ×SBCEF×1=
×SBCEF×1=
 ,
,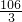 .
. ,利用M到平面ABCD的距离为1,即可求得直线AM与平面ABCD所成角的正弦值;
,利用M到平面ABCD的距离为1,即可求得直线AM与平面ABCD所成角的正弦值; ,EF=2,即可求得二面角A-MN-C的平面角;
,EF=2,即可求得二面角A-MN-C的平面角;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
某建筑物的上半部分是多面体 , 下半部分是长方体
, 下半部分是长方体 (如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.
(如图). 该建筑物的正视图和侧视图(如图), 其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成.


(Ⅰ)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)求该建筑物的体积.
查看答案和解析>>
科目:高中数学 来源:2012年广东省广州市高考数学二模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012年广东省广州市高考数学二模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com