
如图,点D为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,DM⊥BB1交AA1与点M,DN⊥BB1交CC1于点N.
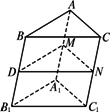
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:
DE2=DF2+EF2-2DF·EFcos∠DFE,拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并加以证明.
科目:高中数学 来源: 题型:013
如图所示,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠BAC=90°且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )
A.直线AC上
B.直线AB上
C.直线BC上
D.△ABC的内部

查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
A.直线AC上
B.直线AB上
C.直线BC上
D.△ABC的内部

查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
如图所示,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠BAC=![]() ,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在
,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在

[ ]
查看答案和解析>>
科目:高中数学 来源:2013届天津市高二上学期期中考试理科数学试卷 题型:选择题
如图所示,在斜三棱柱ABC-A1B1C1的底面△ABC中,∠A=90°,且BC1⊥AC,过C1作C1H⊥底面ABC,垂足为H,则点H在( )
A.直线AB上
B.直线AC上
C.直线BC上
D.△ABC内部

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com