
设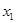 、
、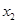
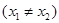 是函数
是函数 的两个极值点.
的两个极值点.
(1)若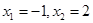 ,求函数
,求函数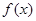 的解析式;
的解析式;
(2)若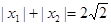 ,求
,求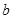 的最大值;
的最大值;
(3)设函数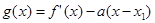 ,
,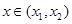 ,当
,当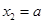 ,求证:
,求证: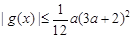
(1)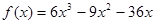
(2)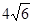
(3)证明略
【解析】解:(1)∵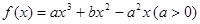 ,∴
,∴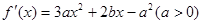
依题意有-1和2是方程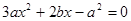 的两根
的两根
∴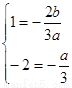 ,. ……………………………3分
,. ……………………………3分
解得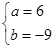 ,
,
∴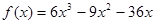 .(经检验,适合). ……………………4分
.(经检验,适合). ……………………4分
(2)∵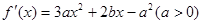 ,
,
依题意,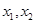 是方程
是方程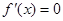 的两个根,∵
的两个根,∵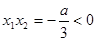 且
且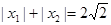 ,
,
∴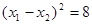 .……………………………6分
.……………………………6分
∴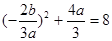 ,∴
,∴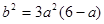 .
.
∵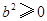 ∴
∴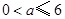 .……………………………7分
.……………………………7分
设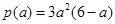 ,则
,则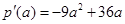 .
.
由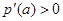 得
得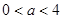 ,由
,由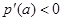 得
得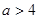 .………………………8分
.………………………8分
即:函数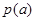 在区间
在区间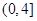 上是增函数,在区间
上是增函数,在区间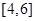 上是减函数,
上是减函数,
∴当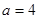 时,
时,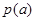 有极大值为96,∴
有极大值为96,∴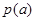 在
在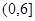 上的最大值是96,
上的最大值是96,
∴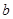 的最大值为
的最大值为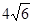 . ……………………………9分
. ……………………………9分
(3) 证明:∵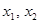 是方程
是方程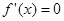 的两根,
的两根,
∴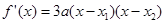 . .………………………10分
. .………………………10分
∵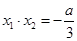 ,
,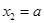 ,∴
,∴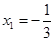 .
.
∴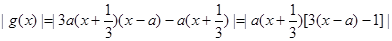 ………12分
………12分
∵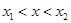 ,即
,即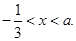 ∴
∴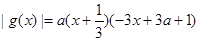 ………13分
………13分
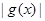
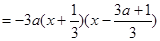
 ……14分
……14分
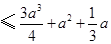
 .
.
∴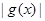
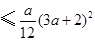 成立. ……………………………16分
成立. ……………………………16分


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:2013届浙江省宁波四校高二下学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分14分)设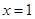 与
与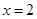 是函数
是函数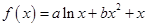 的两个极值点.
的两个极值点.
(1)试确定常数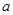 和
和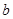 的值;
的值;
(2)试判断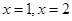 是函数
是函数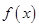 的极大值点还是极小值点,并说明理由。
的极大值点还是极小值点,并说明理由。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三上学期第四次月考文科数学卷 题型:解答题
(本题满分12分)
设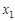 ,
,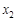 是函数
是函数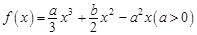 的两个极值点,且
的两个极值点,且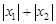
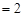 ..
..
(Ⅰ)用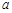 表示
表示 ,并求
,并求 的最大值;
的最大值;
(Ⅱ)若函数 ,求证:当
,求证:当 且
且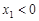 时,
时,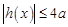
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第一次月考理科数学卷 题型:解答题
(本题满分12分)
设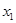 、
、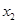
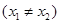 是函数
是函数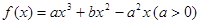 的两个极值点.
的两个极值点.
(1)若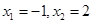 ,求函数
,求函数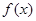 的解析式;
的解析式;
(2)若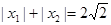 ,求
,求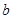 的最大值;
的最大值;
(3)设函数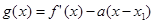 ,
,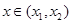 ,当
,当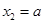 时,
时,
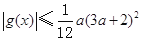 求证:
求证:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com