Question

5．已知函数$f（x）=\left\{\begin{array}{l}{x^2}-mx+m-1\;，\;x≥0\\ f（{x+2}）\;，\;x＜0\end{array}\right.$．
（Ⅰ）当m=8时，求f（-4）的值；
（Ⅱ）当m=8且x∈[-8，8]时，求|f（x）|的最大值；
（Ⅲ）对任意的实数m∈[0，2]，都存在一个最大的正数K（m），使得当x∈[0，K（m）]时，不等式|f（x）|≤2恒成立，求K（m）的最大值以及此时相应的m的值．

Answer 1

分析 （Ⅰ）通过m=8时，直接利用分段函数求f（-4）的值；
（Ⅱ）当m=8且x∈[-8，8]时，画出函数的图象，利用二次函数以及周期函数，转化求解函数|f（x）|的最大值；
（Ⅲ） ①当m=0时，f（x）=x²-1（x≥0），转化求解即可，②当0＜m≤2时，求出对称轴，要使得|f（x）|≤2，判断f（x）=x²-mx+m-1（x≥0）与y=-2的位置关系，
通过比较根的大小，利用函数的单调性求解即可．

解答 （本小题满分15分）
解：（Ⅰ） 当m=8时，f（-4）=f（-2）=f（0）=7-------------------（2分）
（Ⅱ）函数$f（x）=\left\{\begin{array}{l}{x^2}-mx+m-1\;，\;x≥0\\ f（{x+2}）\;，\;x＜0\end{array}\right.$．
 0≤x≤8时，函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-8x+7，x≥0}\\{f（x+2），x＜0}\end{array}\right.$．
f（x）=x²-8x+7，当x=4时，函数取得最小值-9，x=0或x=8时函数取得最大值：7，
f（x）∈[-9，7]--------------------（3分）
-8≤x＜0时，f（x）=f（x+2），如图函数图象，f（x）∈（-5，7]--------------------（4分）
所以x∈[-8，8]时，|f（x）|_max=9--------------------（5分）
（能清晰的画出图象说明|f（x）|的最大值为9，也给3分）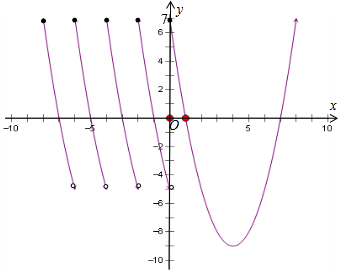

（Ⅲ） ①当m=0时，f（x）=x²-1（x≥0），要使得|f（x）|≤2，
只需x²-1≤2，得$x≤\sqrt{3}$，即$K（m）=\sqrt{3}$，此时m=0-----------（7分）
②当0＜m≤2时，对称轴$x=\frac{m}{2}∈（{0\;，\;1}]$，要使得|f（x）|≤2，
首先观察f（x）=x²-mx+m-1（x≥0）与y=-2的位置关系，
由x²-mx+m-1≥-2对于0＜m≤2恒成立，-----------（9分）
故K（m）的值为x²-mx+m-1=2的较大根x₂，
解得${x_2}=\frac{{m+\sqrt{{m^2}-4m+12}}}{2}$-----------（10分）
又${x_2}=\frac{{m-2+\sqrt{{m^2}-4m+12}}}{2}+1$=$\frac{{\sqrt{{m^2}-4m+12}-（2-m）}}{2}+1$
=$\frac{8}{{2[{\sqrt{{m^2}-4m+12}+（2-m）}]}}+1$-----------（12分）
故$K（m）=\frac{8}{{2[{\sqrt{{m^2}-4m+12}+（2-m）}]}}+1$，
则显然K（m）在m∈（0，2]上为增函数，
所以${[{K（m）}]_{max}}=k（2）=1+\sqrt{2}$-----------（15分）
由①②可知，K（m）的最大值为$1+\sqrt{2}$，此时m=2．

点评 本题考查函数的图形的综合应用，二次函数以及周期函数的应用，考查转化思想以及计算能力．