练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点A(1－t，1－t，t)，B(2，t，t)，则|AB|的最小值是________．

    答案：
    解析：


    提示：

    |AB|＝＝，当t＝时，|AB|有最小值．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点A（1-t，1-t，t），B（2，t，t），则A、B两点距离的最小值为（　　）

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练23练习卷（解析版） 题型：解答题

    在平面直角坐标系xOy中,已知点A(-1,-2),B(2,3),C(-2,-1).

    (1)求以线段AB、AC为邻边的平行四边形的两条对角线的长;

    (2)设实数t满足(-t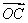)·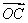=0,求t的值.

     

    查看答案和解析>>

    科目：高中数学 来源：江苏高考真题 题型：解答题

    在平面直角坐标系xOy中，已知点A(-1，-2)，B(2，3)，C(-2，-1)，
    (Ⅰ)求以线段AB、AC为邻边的平行四边形的两条对角线的长；
    (Ⅱ)设实数t满足，求t的值。

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年浙江省杭州市学军中学高三（上）期中数学试卷（理科）（解析版） 题型：解答题

    已知点（1，）是函数f（x）=ax（a＞0且a≠1）的图象上一点，等比数列{an}的前n项和为f（n）-c，数列{bn}（bn＞0）的首项为c，且前n项和Sn满足Sn-Sn-1=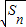+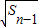（n≥2）．记数列{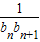}前n项和为Tn，
    （1）求数列{an}和{bn}的通项公式；
    （2）若对任意正整数n，当m∈[-1，1]时，不等式t2-2mt+＞Tn恒成立，求实数t的取值范围
    （3）是否存在正整数m，n，且1＜m＜n，使得T1，Tm，Tn成等比数列？若存在，求出m，n的值，若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案