设集合A={x|1-a≤x≤1+a},集合B={x|x<-1或x>5},分别就下列条件求实数a的取值范围:
(1)A∩B=∅;
(2)A∪B=B.
解:(1)∵A={x|1-a≤x≤1+a},集合B={x|x<-1或x>5},且A∩B=∅,
∴A=∅或A的解集为-1≤x≤5,即1-a>1+a或
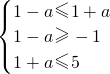
,
解得:a<0或0≤a≤2,
则当A∩B=∅时,a的取值范围为a≤2;
(2))∵A∪B=B,∴A⊆B,
依题意得:1-a>5或1+a<-1,
解得:a<-4或a<-2,
则当A∪B=B时,a的取值范围为a<-2.
分析:(1)由集合A和B,且A与B的交集为空集,得到A为空集或A的解集为-1≤x≤5,列出关于a的不等式及不等式组,求出不等式及不等式组的解集,即可得到A∩B=∅时,a的取值范围;
(2)由A与B的并集为B,得到A为B的子集,根据集合A和B中不等式的解集,列出关于a的不等式,求出不等式的解集,即可得到满足题意a的范围.
点评:此题考查了交集、并集的运算,以及集合间的包含关系,弄清题意是解本题的关键.

 ,
,
