
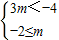 ,解可得-2≤m<-
,解可得-2≤m<- ,
, ).
).

 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年贵州省六盘水市高三10月月考文科数学(解析版) 题型:解答题
(本小题满分10分) 已知全集为R,A={x|x2-x-6≤0},B={x|x2+2x-8>0},C={x|x2-4mx+3m2<0,m<0}.
(1)求A∩B;
(2)如果(∁RA)∩(∁RB)⊆C,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011年江西省高一下学期期中考试数学 题型:解答题
(本题满分12分)
已知全集为R,A={x|log2(3-x)≤2},B={x|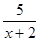 ≥1},求CR(A∩B)
≥1},求CR(A∩B)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com