
已知函数f(x)=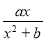 在x=1处取得极值2.
在x=1处取得极值2.
(1)求函数f(x)的表达式;
(2)当m满足什么条件时,函数f(x)在区间(m,2m+1)上单调递增?
(1)f(x)=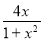 ;(2)m∈(﹣1,0].
;(2)m∈(﹣1,0].
【解析】
试题分析:(1)由已知可得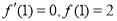 ,可得关于a,b的二元方程组,解此方程组可求得a,b的值.
,可得关于a,b的二元方程组,解此方程组可求得a,b的值.
(2)先利用导数求出f(x)的增区间,由条件可知(m,2m+1)为f(x)增区间的子集,从而可求得m所满足的条件.
试题解析:(1)因为f′(x)=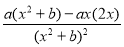 ,而函数f(x)=
,而函数f(x)=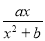 在x=1处取得极值2,所以
在x=1处取得极值2,所以 ,即
,即 ,解得
,解得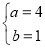 .
.
故f(x)=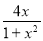 即为所求.
即为所求.
(2)由(1)知f′(x)=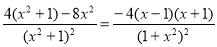 ,令f′(x)>0,得﹣1<x<1,∴f(x)的单调增区间为[﹣1,1].
,令f′(x)>0,得﹣1<x<1,∴f(x)的单调增区间为[﹣1,1].
由已知得 ,解得﹣1<m≤0.
,解得﹣1<m≤0.
故当m∈(﹣1,0]时,函数f(x)在区间(m,2m+1)上单调递增.
考点:1.函数的极值概念;2.利用导数研究函数的单调性.


科目:高中数学 来源:2015届陕西省宝鸡市金台区高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设函数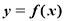 ,用二分法求方程
,用二分法求方程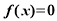 在
在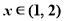 内近似解的过程中得
内近似解的过程中得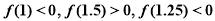 则方程的根落在区间 ( )
则方程的根落在区间 ( )
A.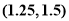 B.
B.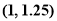 C.
C.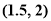 D.不能确定
D.不能确定
查看答案和解析>>
科目:高中数学 来源:2015届陕西省咸阳市高二下学期期末质量检测理科数学试卷(解析版) 题型:填空题
(2009•聊城一模)由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“ •
•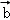 =
=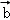 •
• ”;
”;
②“(m+n)t=mt+nt”类比得到“( +
+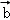 )•
)•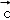 =
= •
•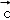 +
+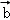 •
•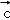 ”;
”;
③“t≠0,mt=nt⇒m=n”类比得到“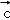 ≠0,
≠0,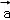 •
•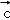 =
=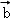 •
•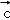 ⇒
⇒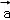 =
=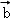 ”;
”;
④“|m•n|=|m|•|n|”类比得到“|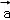 •
•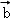 |=|
|=|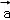 |•|
|•|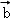 |”.
|”.
以上类比得到的正确结论的序号是 _________ (写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源:2015届陕西省咸阳市高二下学期期末质量检测理科数学试卷(解析版) 题型:选择题
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n﹣mi)为实数的概率为( )
A. B.
B. C.
C.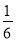 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届重庆市高二下期期中考试文科数学试卷(解析版) 题型:选择题
设双曲线 的两条渐近线与直线
的两条渐近线与直线 分别交于A,B两点,F为该双曲线的右焦点.若
分别交于A,B两点,F为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是( )
, 则该双曲线的离心率的取值范围是( )
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com