
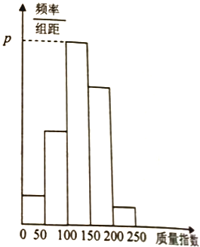
 中华人民共和国关于《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)中,关于空气质量指数划分如下表所示:
中华人民共和国关于《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)中,关于空气质量指数划分如下表所示:| AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 级别 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | Ⅴ级 | Ⅵ级 |
| 类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 分组 | 频数 | 频率 |
| [0,50) | x | 0.06 |
| [50,100) | 10 | 0.2 |
| {100,150) | 20 | y |
| [150,200) | 15 | 0.3 |
| [200,250) | 2 | 0.04 |
| 合计 | n | 1 |
| 10 |
| 0.2 |
| 20 |
| 50 |
| 0.4 |
| 50 |
. |
| x |


科目:高中数学 来源: 题型:
| 3 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、f(-
| ||
B、f(0)<f(-
| ||
C、f(0)<f(3)<f(-
| ||
D、f(3)<f(0)<f(-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1+ax |
| 1-x |
| 2 |
| x2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3-a |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com