
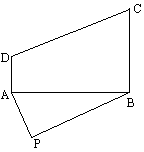
如图所示,某农场在P处有一个肥堆,今要把这堆肥料沿道路PA或PB送到大田ABCD中去.已知PA=100米,PB=150米,∠APB=![]() ,能否在大田中确定一条界线,使位于界线一侧的点沿道路PA送肥较近,而另一侧的点则沿道路PB送肥较近?如果能,请说出这条界线是一条什么曲线,并求出其方程。
,能否在大田中确定一条界线,使位于界线一侧的点沿道路PA送肥较近,而另一侧的点则沿道路PB送肥较近?如果能,请说出这条界线是一条什么曲线,并求出其方程。
|
解:大田ABCD中的点可分为三类:第一类沿PA送肥较近,第二类沿PB送肥较近,第三类沿PA或PB送肥一样远近.由题意知,界线是第三类点的轨迹. 设M是界线上任一点,则|PA|+|MA|=|PB|+|MB|, 即|MA|-|MB|=|PB|-|PA| =150-100=50(定值). 因此,所求界线是以A、B为焦点的双曲线的一支. 以直线AB为x轴,线段AB的中点O为坐标原点,如图建立直角坐标系,则所求曲线方程标准形式为 其中a=25. 2c=|AB| = =50 c=25 因此,所求双曲线方程为 分析:由题意列出几何等式,借助于圆锥曲线的定义解题. 点评:在分析几何因素时,将|PA|+|MA|=|PB|+|MB|转化为|MA|-|MB|-|PB|-|PA|为定值是解题的关键. |


科目:高中数学 来源:设计选修数学-1-1苏教版 苏教版 题型:044
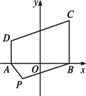
如图所示,某农场在P处有一肥堆,今要把这堆肥沿道路PA或PB送到大田ABCD中去,已知AP=100 m,PB=150 m,∠APB=60°,能否在大田中确定一条界线,使位于界线一侧的点沿PA送肥较近,而另一侧的点沿PB送肥较近?如能,请确定这条界线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com