Question

（mx+1）⁷的展开式中，x³项的系数是x²项的系数和x⁵项系数的等比中项，则m=    ．

Answer 1

【答案】分析：先求出展开式的通项，求出x³，x²，x⁵的系数，然后根据等比中项建立等式关系，解之即可求出所求．
解答：解：（mx+1）⁷展开式的通项为T_r+1=C_b^r（mx）^r=m^rC₇^rx^r
x³，x²，x⁵的系数分别是m³C₇³，m²C₇²，m⁵C₇⁵
∴（m³C₇³）²=m²C₇²•m⁵C₇⁵解得m=
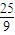
故答案为：．
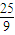
点评：本题主要考查了二项式定理的应用，同时考查了等比中项的性质，属于基础题．