
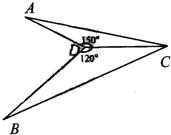
 如图,∠ADC=150°,∠BDC=120°,AD=1,BD=
如图,∠ADC=150°,∠BDC=120°,AD=1,BD=| 3 |
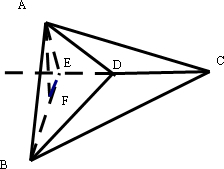 解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,
解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
| AF2+BF2 |
| ||
| 2 |
| AF |
| AB |
| ||||
|
| ||
| 14 |
| ||
| 14 |


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
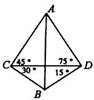 我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).
(2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )
如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )查看答案和解析>>
科目:高中数学 来源: 题型:
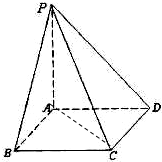 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AD⊥AB,PA=
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,AD⊥AB,PA=| 6 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com