
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
分析 求出f(x)的导数,得到函数的单调区间,从而比较函数值的大小即可.
解答 解:f(x)=x2+cosx,f′(x)=2x-sinx,f″(x)=2-cosx>0,
∴f′(x)在R递增,而f′(0)=0,
∴x∈(-∞,0)时,f′(x)<0,f(x)递减,
x∈(0,+∞)时,f′(x)>0,f(x)递增,
而f(-x)=x2+c0s(-x)=x2+cosx=f(x),
∵log${\;}_{\frac{1}{2}}$$\frac{1}{4}$=2,log2$\frac{\sqrt{2}}{2}$=-$\frac{1}{2}$,
∴f(log2$\frac{\sqrt{2}}{2}$)=f(-$\frac{1}{2}$)=f($\frac{1}{2}$),
∵$\frac{1}{2}$<1<2,
∴f($\frac{1}{2}$)<f(1)<f(2),
∴c<a<b,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用以及函数的奇偶性问题,是一道中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
无穷等比数列 中,“
中,“ ”是“数列
”是“数列 为递减数列”的( )
为递减数列”的( )
A.充分而不必要条件 B.充分必要条件
C.必要而不充分条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
圆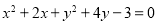 上到直线
上到直线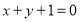 的距离为
的距离为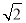 的点共有( )
的点共有( )
A.1个 B.2个 C. 3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
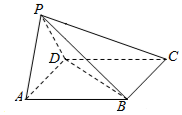 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,四边形ABCD是平行四边形,∠ADC=120°,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com