

 的体积为
的体积为 .
. ∥平面
∥平面 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证 ∥平面
∥平面 ,根据直线与平面平行的判定定理可知只需证
,根据直线与平面平行的判定定理可知只需证 与平面
与平面 内一直线平行,取
内一直线平行,取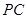 的中点
的中点 ,连接
,连接 ,易证
,易证 ,从而得
,从而得 ∥平面
∥平面 ;(2)求三棱锥
;(2)求三棱锥 的体积,三棱锥
的体积,三棱锥 的体积可转化成三棱锥
的体积可转化成三棱锥 的体积,而
的体积,而 底面
底面 ,从而
,从而 即为三棱锥
即为三棱锥 的高,根据三棱锥的体积公式进行求解即可.
的高,根据三棱锥的体积公式进行求解即可. 又E为AB的中点,ABCD是正方形,
又E为AB的中点,ABCD是正方形, 故AE∥GF且
故AE∥GF且
 平面
平面 ,
, 平面
平面 ,所以,AF∥平面
,所以,AF∥平面 .
.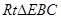 的面积为1,故
的面积为1,故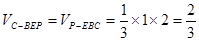 .
. .
.

科目:高中数学 来源:不详 题型:单选题
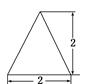
A.4 ,8 ,8 | B.4 , , |
C.4( +1), +1), | D.8,8 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
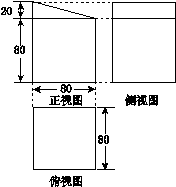
| A.40 000 cm2 | B.40 800 cm2 |
C.1600(22+ )cm2 )cm2 | D.41 600 cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com