
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
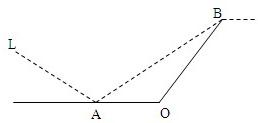 某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.
某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.
如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.查看答案和解析>>
科目:高中数学 来源: 题型:
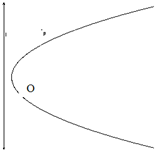 如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案.(作出图形),并求公路总长的最小值(精确到0.001千米)
如图,弯曲的河流是近似的抛物线C,公路l恰好是C的准线,C上的点O到l的距离最近,且为0.4千米,城镇P位于点O的北偏东30°处,|OP|=10千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路l,以便建立水陆交通网.为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案.(作出图形),并求公路总长的最小值(精确到0.001千米)查看答案和解析>>
科目:高中数学 来源:设计选修数学-4-5人教A版 人教A版 题型:044
公路的两侧要修建一些加油站,两个加油站位于某城市东a km和b km处(a<b),一卡车从该城市出发,由于某种原因,他需要往返A、B两加油站,问他行驶在什么情况下到两加油站的路程之和是一样的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com