
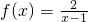 .
.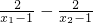
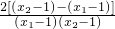 =
=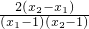 .
.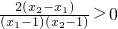 ,即f(x1)-f(x2)>0.
,即f(x1)-f(x2)>0. .
.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修3) 2009-2010学年 第32期 总188期 北师大课标版 题型:013
下列算法:
①求和:1+2+3+…+1000;
②已知两个数求它们的商;
③已知函数定义在区间上,将区间十等分求端点及各分点处的函数值;
④已知三角形的一边长及此边上的高,求其面积.其中可能要用到循环结构的是
①②
①③
①④
③④
查看答案和解析>>
科目:高中数学 来源:“伴你学”新课程 数学·必修3、4(人教B版) 人教B版 题型:013
下列算法:
①求和1+2+3+…+1000;
②已知两个数求它们的商;
③已知函数f(x)定义在区间[a,b]上,将区间[a,b]十等分,求端点及各分点处的函数值;
④已知三角形的三边求其面积.
其中可能要用到循环结构的是
A.①②
B.①③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源:2014届云南省高一上学期期中数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
【解析】第一问利用函数的奇函数性质可知f(0)=0
结合条件 ,解得函数解析式
,解得函数解析式
第二问中,利用函数单调性的定义,作差变形,定号,证明。
第三问中,结合第二问中的单调性,可知要是原式有意义的利用变量大,则函数值大的关系得到结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com