
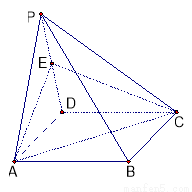
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)证明:PB//平面EAC;
(2)若AD=2AB=2, 求直线PB与平面ABCD所成角的正切值;
(1)详见解析;(2)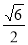 .
.
【解析】
试题分析:(1)要证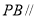 平面
平面 ,根据线面平行的判定定理,只需证明
,根据线面平行的判定定理,只需证明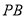 平行于平面
平行于平面 中的一条直线.连接
中的一条直线.连接 交
交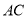 于
于 ,连接
,连接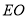 ,因为
,因为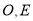 分别为
分别为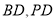 的中点,根据三角形的中位线的性质,可知
的中点,根据三角形的中位线的性质,可知 ,从而问题得证;
,从而问题得证;
(2)设 为
为 中点,连接
中点,连接 ,则
,则 ,从而可得
,从而可得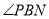 为直线
为直线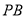 与平面
与平面 所成的角,进而可求
所成的角,进而可求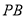 与平面
与平面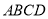 所成角正切值;
所成角正切值;
【解析】
(1)连结BD交AC于O,连结EO,
因为O、E分别为BD、PD的中点, 所以EO//PB, 2分
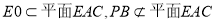 ,所以PB//平面EAC。 5分
,所以PB//平面EAC。 5分
(2)设N为AD中点,连接PN,则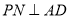 6分
6分
又面PAD⊥底面ABCD,所以,PN⊥底面ABCD 7分
所以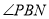 为直线PB与平面ABCD所成的角, 8分
为直线PB与平面ABCD所成的角, 8分

 又AD=2AB=2,则PN=
又AD=2AB=2,则PN= , 10分
, 10分
所以tan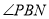 =
= , 12分;所以PB与平面ABCD所成角正切为值
, 12分;所以PB与平面ABCD所成角正切为值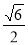 13分
13分
考点:1.线与平面平行的判定;2.直线与平面所成的角.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2016届山西省高一下学期期中考试数学试卷(解析版) 题型:选择题
在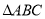 中,若
中,若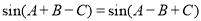 ,则
,则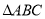 必是( )
必是( )
A.等腰三角形 B.直角三角形
C.等腰或直角三角形 D.等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2016届山东省滨州市高一下学期期末考试数学试卷(解析版) 题型:选择题
在等差数列{an}中,若a3+a7=10,则等差数列{an}的前9项和S9等于( ).
A.45 B.48 C.54 D.108
查看答案和解析>>
科目:高中数学 来源:2016届山东省高一下学期期中考试数学试卷(解析版) 题型:填空题
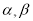 是两个不同的平面,
是两个不同的平面, 是平面
是平面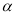 及
及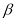 之外的两条不同直线,给出四个论断:
之外的两条不同直线,给出四个论断:
①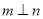 ②
②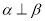 ③
③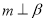 ④
④ 。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
。 以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:________________________________.
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一二月检测数学试卷(解析版) 题型:选择题
已知函数y=sin(ωx+φ)(ω>0,|φ|<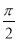 )的部分图象如图所示,则( )
)的部分图象如图所示,则( )

A.ω=2,φ=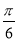 B.ω=1,φ=-
B.ω=1,φ=-
C.ω=1,φ= D.ω=2,φ=-
D.ω=2,φ=-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com