Question

设f（x）在定义域A上是单调递减函数，又F（x）=a^f（x）（a＞0），当f（x）＞0时，F（x）＞1．
求证：（1）f（x）＜0时，F（x）＜1；
（2）F（x）在定义域A上是减函数．

Answer 1

证明：（1）∵f（x）＞0时，F（x）=a^f（x）＞1，
∴a＞1
则f（x）＜0时，-f（x）＞0…（2分）
∴a^-f（x）＞1
∴
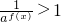
∴0＜a^f（x）＜1
∴F（x）＜1…（4分）
（2）设x₁＜x₂，x₁．x₂∈A…（5分）
∵f（x）在A上为减函数，
∴f（x₁）＞f（x₂）
即f（x₂）-f（x₁）＜0，
而F（x₂）-F（x₁）=a^f（x2）-a^f（x1）=a^f（x1）[a^{f（x2）-f（x1）}-1]…（8分）
∵a＞0，
∴a^f（x1）＞0，且当f（x₂）-f（x₁）＜0
而f（x）＜0时，F（x）＜1
∴a^{f（x2）-f（x1）}＜1
∴F（x₂）-F（x₁）＜0∴F（x₂）＜F（x₁）
∴F（x）在定义域A上是减函数…（13分）
分析：（1）由已知中F（x）=a^f（x）（a＞0），当f（x）＞0时，F（x）＞1．我们可以判断出底数a＞1，进而根据指数函数的性质，可以得到f（x）＜0时，F（x）＜1；
（2）x₁＜x₂，x₁．x₂∈A，根据f（x）在定义域A上是单调递减函数，可得f（x₂）-f（x₁）＜0，进而判断出F（x₂）-F（x₁）的符号，进而根据函数单调性的定义即可得到F（x）在定义域A上是减函数．
点评：本题考查的知识点是函数单调性的判断与证明，指数型复合函数的性质及应用，其中（1）的关键是判断出底数a＞1，进而转化为指数函数性质应用问题，（2）的关键是熟练掌握定义法（做差法）证明函数单调性的方法和步骤．