
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-\sqrt{2}$ |
分析 利用双曲线、椭圆的定义,求出a,利用双曲线的性质,求出c,即可求出椭圆C1的离心率.
解答 解:由题意,不妨设P在第一象限,
∵|PF2|=2,∴|PF1|=6,
∴2a=|PF2|+|PF2|=8,
∴a=4.
∵双曲线C2:x2-y2=4可化为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1,
∴c=$\sqrt{4+4}$=2$\sqrt{2}$
∵椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)与双曲线C2:x2-y2=4有相同的右焦点F2,
∴c=2$\sqrt{2}$,
∴椭圆C1的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故选:B.
点评 本题考查椭圆与双曲线的几何性质,解题的关键是正确运用离心率的定义,属于基础题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
若集合 满足
满足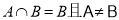 ,则命题“
,则命题“ ”是命题“
”是命题“ ”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
”的 条件.(填“充分不必要”,“必要不充分”,“充要”)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | lga>lgb | D. | $\sqrt{a}$>$\sqrt{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{{6\sqrt{13}}}{13}$ | C. | $\frac{{4\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<log2x<${({\frac{1}{2}})^x}$ | B. | 2x<${({\frac{1}{2}})^x}$<log2x | C. | ${({\frac{1}{2}})^x}$<log2x<2x | D. | log2x<${({\frac{1}{2}})^x}$<2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com