
在面积为9的三角形ABC中,tanA=-![]() ,且
,且![]()
(1)建立适合的坐标系,求以AB、AC所在直线为渐近线且过点D的双曲线的方程.
(2)过D分别作AB、AC所在直线的垂线DE、DF(E、F为垂足),求![]() 的值.
的值.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:044
下列对应,哪些是映射?是映射的哪些原象总是唯一的?哪些是一一映射?
(1) A={x|x∈R},B={y|y∈R+},对应法则f:x→y=![]() .
.
(2) A={x|x∈R},B={x|x∈R+},对应法则f:x→y=|x|.
(3) A={x|x≥0},B={0,1},对应法则f:x→y=x0.
(4) A={x|0≤x≤4},B={y|0≤y≤2},对应法则f:x→y=![]() .
.
(5) A={x|0≤x≤4},B={y|0≤y≤2},对应法则f:x→y=![]() .
.
(6) A={2,3},B={6,12,18},对应法则f:a→b(b被a整除).
(7) A={x|x为平面上的多边形},B={y|y∈R},对应法则f:x→y是x的面积.
(8) A={(x,y)|x,y∈R},B={x|x∈R},对应法则f:(x,y)→x(即让平面上的点与它在x轴上的射影对应).
(9) A={x|1≤x≤2},B={y|a≤y≤b},对应法则f:x→y=(b-a)x+2a-b.
(10) A={(a,b,c)|0<a≤b≤c且c<a+b},B={三角形},对应法则f:(a,b,c) →按逆时针方向顺次以a、b、c为边的三角形.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1) A={x|x∈R},B={y|y∈R+},对应法则f:x→y=![]() .
.
(2) A={x|x∈R},B={x|x∈R+},对应法则f:x→y=|x|.
(3) A={x|x≥0},B={0,1},对应法则f:x→y=x0.
(4) A={x|0≤x≤4},B={y|0≤y≤2},对应法则f:x→y=![]() .
.
(5) A={x|0≤x≤4},B={y|0≤y≤2},对应法则f:x→y=![]() .
.
(6) A={2,3},B={6,12,18},对应法则f:a→b(b被a整除).
(7) A={x|x为平面上的多边形},B={y|y∈R},对应法则f:x→y是x的面积.
(8) A={(x,y)|x,y∈R},B={x|x∈R},对应法则f:(x,y)→x(即让平面上的点与它在x轴上的射影对应).
(9) A={x|1≤x≤2},B={y|a≤y≤b},对应法则f:x→y=(b-a)x+2a-b.
(10) A={(a,b,c)|0<a≤b≤c且c<a+b},B={三角形},对应法则f:(a,b,c) →按逆时针方向顺次以a、b、c为边的三角形.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省泸州市高三第一次教学质量诊断性考试文科数学试卷(解析版) 题型:选择题
若曲线 在点
在点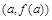 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则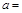 ( )
( )
A.3 B.6 C.9 D.18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com