解:(1)直线的极坐标方程为
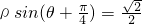
,
即
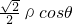
+
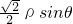
=

,化为直角坐标为 x+y=1.
故极点到该直线的距离为
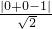
=

.
故答案为

.
(2)∵lga+lgb=0,∴ab=1,且a、b都为正数.
由于
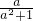
≤

=

,当且仅当a=1时,等号成立.同理可得
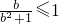
,
∴
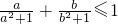
.
不等式
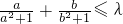
的实数λ的范围是 λ≥1,
故答案为[1,+∞).
(3)解:连接OO′,AO′,B0′,设圆的半径为r
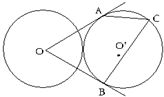
根据切线的性质可得AO′⊥AO,BO′⊥BO
由两圆相外切可得,OO′=2r,AO′=BO′=r
∴∠AOO′=∠BOO′=30°,∠AO′B=2×60°=120°
由圆周角定理可得,∠ACB=

∠AO′B=60°
故答案为 60°.
分析:(1)把直线、曲线的极坐标方程化为直角坐标方程,利用点到直线的距离公式求出极点到该直线的距离.
(2)由条件可得ab=1,且a、b都为正数,利用基本不等式求出
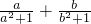
的最大值,从而得到实数λ的范围.
(3)连接OO′,AO′,B0′,设圆的半径为r,根据切线的性质可得AO′⊥AO,BO′⊥BO,由两圆相外切可得,OO′=2r,AO′=BO′=r,从而有∠AOO′=∠BOO′=30°,∠AO′B=2×60°=120°,由圆周角定理可得∠ACB=

∠AO′B的值
点评:本题主要考查了极坐标方程化为直角坐标方程的方法,点到该直线的距离公式,基本不等式的应用,圆的切线的性质、两圆相外切的性质、圆周角定理的综合应用,属于基础题.

 (1)(选修4-4坐标系与参数方程)
(1)(选修4-4坐标系与参数方程)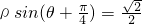 ,则极点到该直线的距离是________.
,则极点到该直线的距离是________.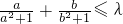 的实数λ的范围是________.
的实数λ的范围是________.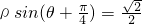 ,
,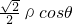 +
+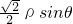 =
= ,化为直角坐标为 x+y=1.
,化为直角坐标为 x+y=1.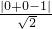 =
= .
. .
.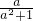 ≤
≤ =
= ,当且仅当a=1时,等号成立.同理可得
,当且仅当a=1时,等号成立.同理可得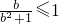 ,
,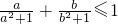 .
.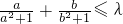 的实数λ的范围是 λ≥1,
的实数λ的范围是 λ≥1,
 ∠AO′B=60°
∠AO′B=60°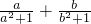 的最大值,从而得到实数λ的范围.
的最大值,从而得到实数λ的范围. ∠AO′B的值
∠AO′B的值
