
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:022
(
江苏东海进修学校模拟)在正方体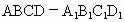 中,过对角线
中,过对角线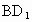 的一个平面交
的一个平面交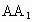 与E,交
与E,交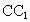 与F,则
与F,则
A.四边形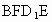 一定是平行四边形;
一定是平行四边形;
B.四边形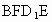 有可能是正方形;
有可能是正方形;
C.四边形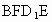 在底面ABCD上的投影一定是正方形;
在底面ABCD上的投影一定是正方形;
D.平面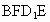 有可能垂直于平面
有可能垂直于平面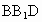 .
.
以上结论正确的是________(按照原顺序填上所有你认为正确的答案的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
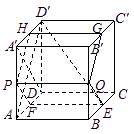 如图,在棱长为1的正方体
如图,在棱长为1的正方体![]() 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥![]() ,截面PQGH∥
,截面PQGH∥![]() .
.
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若![]() 与平面PQEF所成的角为
与平面PQEF所成的角为![]() ,求
,求![]() 与平
与平
面PQGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省遵义四中高一下学期期末考试数学 题型:单选题
“如果一条直线与一个平面垂直,则称这条直线与这个平面构成一组正交线面对;如果两个平面互相垂直,则称这两个平面构成一组正交平面对.”在正方体的12条棱和6个表面中,能构成正交线面对和正交平面对的组数分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市朝阳区高三上学期期末理科数学卷 题型:选择题
如图,正方体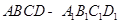 中,
中,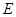 ,
,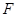 分别为 棱
分别为 棱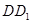 ,
,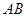 上的点. 已知下列判断:
上的点. 已知下列判断:
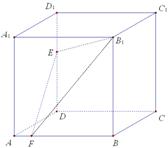
①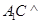 平面
平面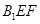 ;②
;②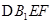 在侧面
在侧面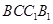 上 的正投影是面积为定值的三角形;③在平面
上 的正投影是面积为定值的三角形;③在平面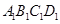 内总存在与平面
内总存在与平面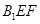 平行的直线;④平 面
平行的直线;④平 面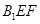 与平面
与平面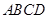 所成的二面角(锐角)的大小与点
所成的二面角(锐角)的大小与点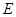 的位置有关,与点
的位置有关,与点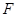 的位置无关.
的位置无关.
其中正确判断的个数有
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:高中数学 来源:2013届贵州省高一下学期期末考试数学 题型:选择题
“如果一条直线与一个平面垂直,则称这条直线与这个平面构成一组正交线面对;如果两个平面互相垂直,则称这两个平面构成一组正交平面对.”在正方体的12条棱和6个表面中,能构成正交线面对和正交平面对的组数分别是( )
(A) 和
和 (B)
(B) 和
和 (C)
(C) 和
和 (D)
(D) 和
和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com