【答案】
分析:(I)设曲线C
1的方程为
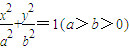
,则根据|AF
1|=

,|AF
2|=

,可得a=3,设A(x,y),F
1(-c,0),F
2(c,0),则(x+c)
2+y
2=
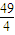
,(x-c)
2+y
2=
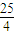
,由此可求曲线C
1和C
2的方程;
(II)过点F
1作直线l垂直于x轴,过点C作直线CC
1⊥l于点C
1,依题意知l为抛物线C2的准线,则|CC
1|=|CF
2|,在△CF
1F
2中,设|CF
2|=r,则|CF
1|=
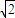
r,|F
1F
2|=2,由余弦定理可得r=2,再利用三角形的面积公式,即可求得结论.
解答:解:(I)设曲线C
1的方程为

,则2a=|AF1|+|AF2|=

得a=3
设A(x,y),F
1(-c,0),F
2(c,0),则(x+c)
2+y
2=

,(x-c)
2+y
2=

两式相减可得:xc=

由抛物线定义可知|AF
2|=x+c=

∴c=1,x=

或x=1,c=

(舍去)
所以曲线C
1的方程为

,C
2的方程为y
2=4x(0≤x≤

);
(II)过点F
1作直线l垂直于x轴,过点C作直线CC
1⊥l于点C
1,依题意知l为抛物线C
2的准线,则|CC
1|=|CF
2|
在直角△CC
1F
1中,|CF
1|=

|CC
1|,∠C
1CF
1=45°

∵∠CF
1F
2=∠C
1CF
1=45°
在△CF
1F
2中,设|CF
2|=r,则|CF
1|=
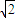
r,|F
1F
2|=2
由余弦定理可得2
2+2r
2-2×2×

rcos45°=r
2,
∴r=2
∴S
△CF1F2=
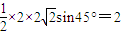 点评:
点评:本题考查了椭圆,抛物线方程的求法,考查三角形面积的计算,求得方程是关键.

 ,|AF2|=
,|AF2|= .
.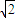 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.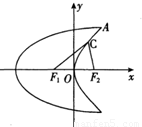
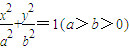 ,则根据|AF1|=
,则根据|AF1|= ,|AF2|=
,|AF2|= ,可得a=3,设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=
,可得a=3,设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=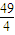 ,(x-c)2+y2=
,(x-c)2+y2=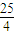 ,由此可求曲线C1和C2的方程;
,由此可求曲线C1和C2的方程;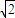 r,|F1F2|=2,由余弦定理可得r=2,再利用三角形的面积公式,即可求得结论.
r,|F1F2|=2,由余弦定理可得r=2,再利用三角形的面积公式,即可求得结论. ,则2a=|AF1|+|AF2|=
,则2a=|AF1|+|AF2|= 得a=3
得a=3 ,(x-c)2+y2=
,(x-c)2+y2=


 或x=1,c=
或x=1,c= (舍去)
(舍去) ,C2的方程为y2=4x(0≤x≤
,C2的方程为y2=4x(0≤x≤ );
); |CC1|,∠C1CF1=45°
|CC1|,∠C1CF1=45°
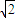 r,|F1F2|=2
r,|F1F2|=2 rcos45°=r2,
rcos45°=r2,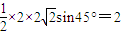


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案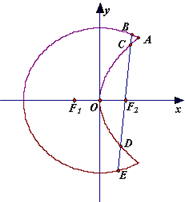 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=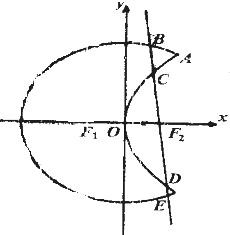 曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,A(
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,A(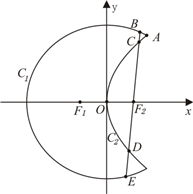 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= 如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,A(
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,A(