
(本题11分)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则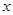 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图3,抛物线上是否存在一点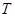 ,过点
,过点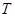 作
作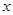 轴的垂线,垂足为
轴的垂线,垂足为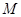 ,过点
,过点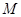 作直线
作直线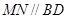 ,交线段
,交线段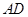 于点
于点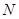 ,连接
,连接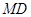 ,使
,使 ~
~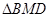 ,若存在,求出点
,若存在,求出点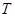 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
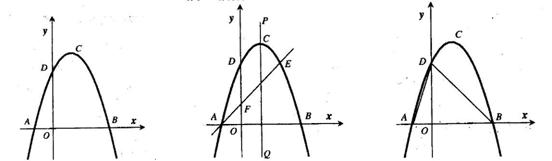 图1
图2
图3
图1
图2
图3
解:(1)设所求抛物线的解析式为: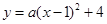 ,依题意,将点B(3,0)代入,得
,依题意,将点B(3,0)代入,得 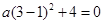 解得:a=-1 ∴所求抛物线的解析式为:
解得:a=-1 ∴所求抛物线的解析式为: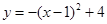
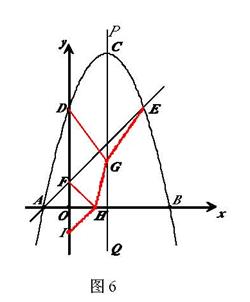
(2)如图6,在y轴的负半轴上取一点I,使得点F与点I关于x轴对称,
在x轴上取一点H,连接HF、HI、HG、GD、GE,则HF=HI…………………①
设过A、E两点的一次函数解析式为:y=kx+b(k≠0),
∵点E在抛物线上且点E的横坐标为2,将x=2代入抛物线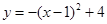 ,得
,得
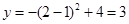
∴点E坐标为(2,3)
又∵抛物线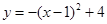 图像分别与x轴、y轴交于点A、B、D
图像分别与x轴、y轴交于点A、B、D
∴当y=0时,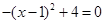 ,∴x=-1或x=3
,∴x=-1或x=3
当x=0时,y=-1+4=3,
∴点A(-1,0),点B(3,0),点D(0,3)
又∵抛物线的对称轴为:直线x=1,
∴点D与点E关于PQ对称,GD=GE…………………②
分别将点A(-1,0)、点E(2,3)代入y=kx+b,得: 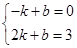
解得: 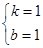
过A、E两点的一次函数解析式为:y=x+1
∴当x=0时,y=1
∴点F坐标为(0,1)
∴ =2………………………………………③
=2………………………………………③
又∵点F与点I关于x轴对称,
∴点I坐标为(0,-1)
∴ ………④
………④
又∵要使四边形DFHG的周长最小,由于DF是一个定值,
∴只要使DG+GH+HI最小即可
由图形的对称性和①、②、③,可知,
DG+GH+HF=EG+GH+HI
只有当EI为一条直线时,EG+GH+HI最小
设过E(2,3)、I(0,-1)两点的函数解析式为: ,
,
分别将点E(2,3)、点I(0,-1)代入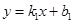 ,得:
,得:
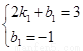
解得: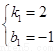
过I、E两点的一次函数解析式为:y=2x-1
∴当x=1时,y=1;当y=0时,x= ;
;
∴点G坐标为(1,1),点H坐标为( ,0)
,0)
∴四边形DFHG的周长最小为:DF+DG+GH+HF=DF+EI
由③和④,可知:
DF+EI=
∴四边形DFHG的周长最小为 。
。
(3)如图7,
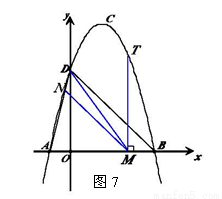
由题意可知,∠NMD=∠MDB,
要使,△DNM∽△BMD,只要使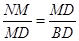 即可,
即可,
即: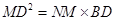 ………………………………⑤
………………………………⑤
设点M的坐标为(a,0),由MN∥BD,可得
△AMN∽△ABD,
∴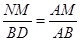
再由(1)、(2)可知,AM=1+a,BD=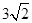 ,AB=4
,AB=4
∴ 
∵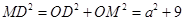 ,
,
∴⑤式可写成: 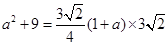
解得 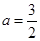 或
或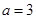 (不合题意,舍去)∴点M的坐标为(
(不合题意,舍去)∴点M的坐标为(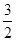 ,0)
,0)
又∵点T在抛物线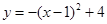 图像上,
图像上,
∴当x=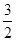 时,y=
时,y=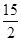 ∴点T的坐标为(
∴点T的坐标为(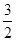 ,
,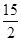 ).
).
【解析】略


科目:高中数学 来源:2012届云南省高三上期中理科数学试卷(解析版) 题型:解答题
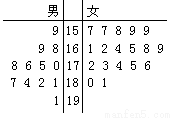
(本题满分12分)第26届世界大学生夏季运动会将于2011年11月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用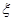 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出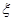 的分布列,并求
的分布列,并求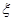 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源:2012年江苏省高一上学期开学考试数学 题型:解答题
(本题11分)如图,矩形ABCD中,AB=6,BC=2 ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;

查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三月考(七)文科数学试卷 题型:解答题
(本题满分12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
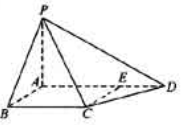
(1) 求证:CE⊥平面PAD;
(11)若PA=AB=1,AD=3,CD=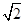 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分11分)张先生家住H小区,他在C科技园区工作,从家开车到公司上班有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为![]() ;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为![]() ,
,![]() .
.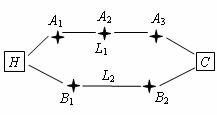
(Ⅰ)若走L1路线,求最多遇到1次红灯的概率;
(Ⅱ)若走L2路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com