
解法一:若直线l:y=x+b和圆x2+y2=2有两个公共点,只有一个公共点,没有公共点,
则方程组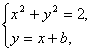 有两个不同解,有两个相同解,没有实数解.
有两个不同解,有两个相同解,没有实数解.
方程组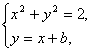 消去y,得2x2+2bx+b2-2=0.
消去y,得2x2+2bx+b2-2=0.
所以Δ=(2b)2-4×2(b2-2)=16-4b2.
所以当Δ=16-4b2>0,即-2<b<2时,圆与直线有两个公共点;
当Δ=16-4b2=0,即b=±2时,圆与直线只有一个公共点;
当Δ=16-4b2<0,即b>2或b<-2时,圆与直线没有公共点.
解法二:圆x2+y2=2的圆心C的坐标为(0,0),半径长为![]() ,圆心C到直线l:y=x+b的距离d=
,圆心C到直线l:y=x+b的距离d=![]() .
.
当d>r时,即![]() >
>![]() ,即|b|>2,即b>2或b<-2时,圆与直线没有公共点;
,即|b|>2,即b>2或b<-2时,圆与直线没有公共点;
当d=r时,即![]() =
=![]() ,即|b|=2,即b=±2时,圆与直线只有一个公共点;
,即|b|=2,即b=±2时,圆与直线只有一个公共点;
当d<r时,即![]() <
<![]() ,即|b|<2,即-2<b<2时,圆与直线有两个公共点.
,即|b|<2,即-2<b<2时,圆与直线有两个公共点.
点评:由于圆的特殊性判断圆与直线的位置关系,多采用判断圆心到直线的距离与半径的大小之间的关系;而以后我们将要学习的圆锥曲线与直线位置关系的判断,则需要利用方程组解的个数来判断.


科目:高中数学 来源: 题型:
| 2 |
A、y=x+
| ||||
B、y=-x+
| ||||
C、y=x+
| ||||
D、x=1或y=x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com