
 已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC=
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC= ,将此图形沿BC折叠成直二面角,连接AF、DE得到几何体(如
,将此图形沿BC折叠成直二面角,连接AF、DE得到几何体(如 和
和 的坐标,进而得到两向量共线,即可证明线面平行.
的坐标,进而得到两向量共线,即可证明线面平行. 解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系.
解:(1)以B为坐标原点,分别以射线BF、BC、BA为x轴、y轴、z轴的正方向建立如图所示的坐标系. ,
, ),E(
),E( ,
, ,0),
,0), =(1,0,-1),
=(1,0,-1), =(
=( ,0,-
,0,- ),
), =
=
 ,∴AF∥DE,
,∴AF∥DE, =(1,0,-1),AD=(0,
=(1,0,-1),AD=(0, ,
, ),
), 垂直于平面ADEF,
垂直于平面ADEF, =(x,y,z),则
=(x,y,z),则 ⇒
⇒ ,
, =(
=( ,-1,
,-1, ),
), =(1,0,0),
=(1,0,0), ,
, >=
>= =
= =
= =
= ,
, =
= =
= .
. .…(12分)
.…(12分)

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
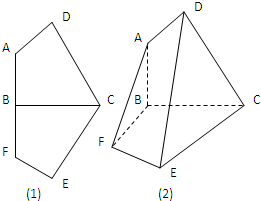 (2012•安徽模拟)已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC=
(2012•安徽模拟)已知轴对称平面五边形ADCEF(如图1),BC为对称轴,ADCD,AD=AB=1,CD=BC=| 3 |
查看答案和解析>>
科目:高中数学 来源:2014届江西师大附中高三年级10月月考理科数学试卷(解析版) 题型:解答题
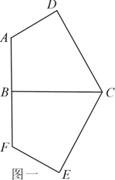
已知轴对称平面五边形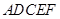 (如图1),
(如图1),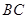 为对称轴,
为对称轴,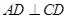 ,
,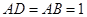 ,
, ,将此图形沿
,将此图形沿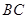 折叠成直二面角,连接
折叠成直二面角,连接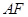 、
、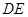 得到几何体(如图2).
得到几何体(如图2).
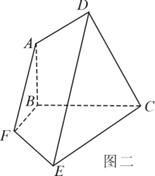
(Ⅰ)证明: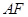 ∥平面
∥平面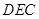 ;
;
(Ⅱ)求二面角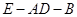 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com