已知A(-1,0),B是圆F:(x-1)2+y2=9(F为圆心)上的一个动点,线段AB的垂直平分线交BF于点P,则动点P的轨迹方程为 .
【答案】
分析:利用线段垂直平分线的性质和椭圆的定义,可证出|PF|+|PA|为定值,且这个定值大于AF长,故点P的轨迹 是以A、F 为焦点的椭圆,然后求出a、b的值得到椭圆的方程,即为所求动点P的轨迹方程.
解答:解:由题意得圆心F(1,0),半径r=3,
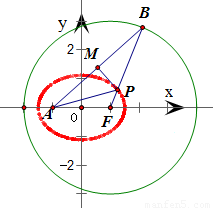
∵线段AB的垂直平分线交BF于点P,
得|PA|=|PB|,
∴|PF|+|PA|=|PF|+|PB|=|BF|=r=3>|AF|,
故点P的轨迹是以A、F 为焦点的椭圆,
其中2a=3,c=1,可得b
2=a
2-c
2=

,
∴椭圆的方程为
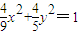
,即为所求动点P的轨迹方程
故答案为:
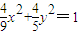 点评:
点评:本题给出圆内满足条件的动点P,求点P的轨迹方程,着重考查了椭圆的定义、线段的中垂线的性质和圆的性质等知识,属于中档题.


 ,
,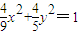 ,即为所求动点P的轨迹方程
,即为所求动点P的轨迹方程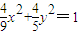


 一线名师提优试卷系列答案
一线名师提优试卷系列答案