Question

已知椭圆的四个顶点恰好是一边长为2，一内角为60°的菱形的四个顶点．

（Ⅰ）求椭圆M的方程；

（Ⅱ）直线l与椭圆M交于A，B两点，且线段AB的垂直平分线经过点，求△AOB（O为原点）面积的最大值．

Answer 1

考点：

直线与圆锥曲线的关系；椭圆的标准方程．

专题：

综合题；圆锥曲线的定义、性质与方程．

分析：

（Ⅰ）依题意，可求得a=，b=1，从而可得椭圆M的方程；

（Ⅱ）设A（x₁，y₁），B（x₂，y₂），依题意，直线AB有斜率，可分直线AB的斜率k=0与直线AB的斜率k≠0讨论，利用弦长公式，再结合基本不等式即可求得各自情况下S_△AOB的最大值．

解答：

解：（Ⅰ）因为椭圆+=1（a＞b＞0）的四个顶点恰好是一边长为2，一内角为60°的菱形的四个顶点，

∴a=，b=1，椭圆M的方程为：+y²=1…4分

（Ⅱ）设A（x₁，y₁），B（x₂，y₂），因为AB的垂直平分线经过点（0，﹣），显然直线AB有斜率，

当直线AB的斜率为0时，AB的垂直平分线为y轴，则x₁=﹣x₂，y₁=y₂，

所以S_△AOB=|2x₁||y₁|=|x₁||y₁|=|x₁|•==，

∵≤=，

∴S_△AOB≤，当且仅不当|x₁|=时，S_△AOB取得最大值为…7分

当直线AB的斜率不为0时，则设AB的方程为y=kx+t，

所以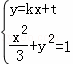，代入得到（3k²+1）x²+6ktx+3t²﹣3=0，

当△=4（9k²+3﹣3t²）＞0，即3k²+1＞t²①，方程有两个不同的实数解；

又x₁+x₂=，=…8分

所以=，又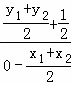=﹣，化简得到3k²+1=4t②

代入①，得到0＜t＜4，…10分

又原点到直线的距离为d=，

|AB|=|x₁﹣x₂|=•，

所以S_△AOB=|AB||d|=••，

化简得：S_△AOB=…12分

∵0＜t＜4，所以当t=2时，即k=±时，S_△AOB取得最大值为．

综上，S_△AOB取得最大值为…14分

点评：

本题考查直线与圆锥曲线的关系，考查椭圆的标准方程，着重考查方程思想分类讨论思想与弦长公式，基本不等式的综合运用，考查求解与运算能力，属于难题．