
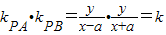 ,由此能够导出动点P的轨迹C的方程.再对k值进行分类讨论:当k>0时,轨迹C为中心在原点,焦点在x轴上的双曲线(除去顶点);当-1<k<0时,轨迹C为中心在原点,焦点在x轴上的椭圆(除去长轴两个端点);当k=-1时,轨迹C为以原点为圆心,1的半径的圆除去点(-1,0),(1,0);当k<-1时,轨迹C为中心在原点,焦点在y轴上的椭圆(除去短轴的两个端点).
,由此能够导出动点P的轨迹C的方程.再对k值进行分类讨论:当k>0时,轨迹C为中心在原点,焦点在x轴上的双曲线(除去顶点);当-1<k<0时,轨迹C为中心在原点,焦点在x轴上的椭圆(除去长轴两个端点);当k=-1时,轨迹C为以原点为圆心,1的半径的圆除去点(-1,0),(1,0);当k<-1时,轨迹C为中心在原点,焦点在y轴上的椭圆(除去短轴的两个端点).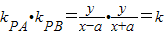 ,
,

 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
| A、①⑤ | B、③④⑤ | C、①②③⑤ | D、①②③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com