Question

18．设F₁，F₂是椭圆E的两个焦点，P为椭圆E上的点，以PF₁为直径的圆经过F₂，若tan∠PF₁F₂=$\frac{{2\sqrt{5}}}{15}$，则椭圆E的离心率为（　　）

• A． $\frac{{\sqrt{5}}}{6}$
• B． $\frac{{\sqrt{5}}}{5}$
• C． $\frac{{\sqrt{5}}}{4}$
• D． $\frac{{\sqrt{5}}}{3}$

Answer 1

分析 由题意画出图形，结合已知及椭圆定义把|PF₁|、|PF₂|用a，c表示，再由勾股定理求得答案．

解答 解：如图，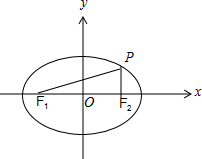
∵以PF₁为直径的圆经过F₂，
∴PF₂⊥F₁F₂，又tan∠PF₁F₂=$\frac{{2\sqrt{5}}}{15}$，
∴$\frac{|P{F}_{2}|}{2c}=\frac{2\sqrt{5}}{15}$，则$|P{F}_{2}|=\frac{4\sqrt{5}}{15}c$，
由|PF₁|+|PF₂|=2a，得|PF₁|=$2a-\frac{4\sqrt{5}}{15}c$，
在Rt△PF₂F₁中，得$（2c）^{2}+（\frac{4\sqrt{5}}{15}c）^{2}=（2a-\frac{4\sqrt{5}}{15}c）^{2}$，
即${e}^{2}+\frac{4\sqrt{5}}{15}e-1=0$，
解得：${e}_{1}=\frac{\sqrt{5}}{3}$或${e}_{2}=-\frac{3\sqrt{5}}{5}$（舍）．
∴椭圆E的离心率为$\frac{\sqrt{5}}{3}$．
故选：D．

点评 本题考查椭圆的简单性质，着重考查椭圆定义的应用，是中档题．